Suma de Fraccionarios | Ejercicios Resueltos
1. Introducción a las Fracciones
A. Definición de fracciones:
Una fracción es una expresión matemática que representa una cantidad que se divide en partes iguales. Se representa como una línea horizontal que divide un número entero en dos partes, una parte superior llamada numerador y una parte inferior llamada denominador. El numerador indica cuántas partes iguales de la cantidad total se están considerando, mientras que el denominador indica en cuántas partes se divide la cantidad total.
Por ejemplo, si queremos representar la fracción que corresponde a la mitad de un objeto, podemos escribirlo como 1/2, donde 1 es el numerador y 2 es el denominador. Esto significa que la cantidad total se ha dividido en dos partes iguales y se está considerando una de ellas.
B. Operaciones básicas con fracciones:
Las operaciones básicas con fracciones son la suma, resta, multiplicación y división. Para sumar o restar fracciones, es necesario que tengan el mismo denominador, si no es así, es necesario buscar un denominador común para poder operar. Para multiplicar fracciones, se multiplican los numeradores y los denominadores. Para dividir fracciones, se multiplica la primera fracción por el inverso multiplicativo de la segunda fracción.Es importante simplificar las fracciones resultantes de estas operaciones, es decir, reducirlas a su mínima expresión, donde el numerador y el denominador no tienen factores comunes mayores que 1.
Por ejemplo, para sumar 1/3 y 2/5, se necesita buscar un denominador común, que en este caso sería 15. Entonces, se convierten ambas fracciones a 15avos, quedando 5/15 y 6/15 respectivamente. Finalmente, se suman los numeradores y se mantiene el denominador común, quedando 11/15.
2. Suma de fracciones con igual denominador
A. Reglas básicas
Cuando se suman fracciones con el mismo denominador, se suman simplemente los numeradores y se conserva el denominador. La regla general para la suma de fracciones con el mismo denominador es la siguiente:
Es importante mencionar que para sumar fracciones, el denominador debe ser el mismo, lo que significa que las fracciones deben tener un denominador común.
B. Ejemplos resueltos
Calcule la suma de las fracciones 3/4 y 5/4.
Solución:
Como las fracciones tienen el mismo denominador, se suman simplemente los numeradores y se conserva el denominador:
3/4 + 5/4 = (3 + 5)/4 = 8/4 = 2
Por lo tanto, la suma de las fracciones 3/4 y 5/4 es igual a 2.
Ejemplo 2:
Calcule la suma de las fracciones 2/5 y 1/5.
Solución:
Como las fracciones tienen el mismo denominador, se suman simplemente los numeradores y se conserva el denominador:
2/5 + 1/5 = (2 + 1)/5 = 3/5Por lo tanto, la suma de las fracciones 2/5 y 1/5 es igual a 3/5.
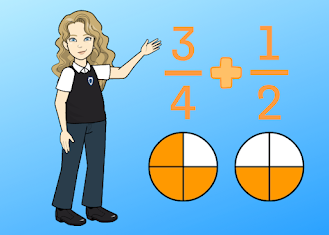
3. Suma de fracciones con denominadores diferentes
Cuando se tienen fracciones con denominadores diferentes, no se pueden sumar directamente. Para sumar estas fracciones, es necesario encontrar un denominador común, que es el mínimo común múltiplo (mcm) de los denominadores. El proceso de sumar fracciones con diferentes denominadores se puede desglosar en los siguientes pasos:
A. Cálculo del mínimo común múltiplo (mcm) de los denominadores:
El mcm de dos o más números es el menor número que es múltiplo de cada uno de ellos. Para calcular el mcm de dos o más denominadores de fracciones, se pueden utilizar varios métodos, como la descomposición en factores primos o la regla del producto. Por ejemplo, si queremos sumar las fracciones 1/2 y 2/3, el mcm de los denominadores 2 y 3 es 6.
B. Reducción de fracciones a un denominador común:
Una vez que se ha encontrado el mcm de los denominadores, es necesario convertir cada fracción a un denominador común. Para hacer esto, se multiplican el numerador y el denominador de cada fracción por el mismo factor que convierte su denominador en el mcm. Por ejemplo, si queremos sumar las fracciones 1/2 y 2/3, y el mcm es 6, entonces la fracción 1/2 se convierte en 3/6 (multiplicando el numerador y el denominador por 3) y la fracción 2/3 se convierte en 4/6 (multiplicando el numerador y el denominador por 2).
C. Reglas para sumar fracciones con diferentes denominadores:
Una vez que se han reducido las fracciones a un denominador común, se suman los numeradores y se mantiene el denominador común. Es importante recordar que las fracciones equivalentes a una fracción dada se suman restando los numeradores y manteniendo el denominador común. Además, es importante simplificar la fracción resultante si es posible.
D. Ejercicios resueltos:
Por ejemplo, para sumar las fracciones 1/2 y 2/3, se sigue el proceso descrito anteriormente. El mcm de 2 y 3 es 6. Para convertir 1/2 en una fracción con denominador 6, se multiplica el numerador y el denominador por 3, obteniendo 3/6. Para convertir 2/3 en una fracción con denominador 6, se multiplica el numerador y el denominador por 2, obteniendo 4/6. Finalmente, se suman las fracciones 3/6 y 4/6, obteniendo 7/6. La fracción resultante no se puede simplificar más, por lo que se considera la respuesta final.