El Rombo en Matemáticas
En la geometría euclidiana, un rombo (◊),en plural rombos, es un cuadrilátero cuyos cuatro lados tienen la misma longitud. Otro nombre es equilátero cuadrilátero, ya que los medios equiláteros que todos sus lados son iguales. El rombo es a menudo llamado un diamante, Cada rombo es un paralelogramo, y un rombo con ángulos rectos es un cuadrado. Es decir es en realidad un tipo especial de paralelogramo. Recordemos que en un paralelogramo cada par de lados opuestos tienen igual longitud. En un rombo, los cuatro lados tienen la misma longitud y éste tiene todas las propiedades de un paralelogramo. Ver la definición de un paralelogramo
Es un poco como un cuadrado que puede "inclinarse" y los ángulos interiores no tienen que ser de 90 °. A veces llamado un "diamante" o forma "pastilla".
Introducción al rombo
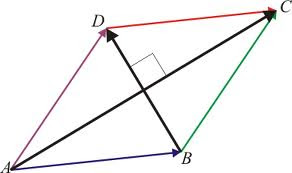
El rombo es un polígono de cuatro lados, donde los lados
opuestos son paralelos y tienen la misma longitud. El rombo tiene cuatro
ángulos iguales y diagonales perpendiculares entre sí que se cruzan en su punto
medio.
Cálculo del perímetro del rombo
El perímetro de un rombo se calcula sumando las longitudes
de sus cuatro lados. Si llamamos a la longitud de cada lado "a",
entonces el perímetro será:
Perímetro = 4*a
Cálculo del área del rombo
El área de un rombo se calcula multiplicando la longitud de
las diagonales y dividiendo el resultado por 2. Si llamamos a las diagonales
"d1" y "d2", entonces el área será:
Área = (d1 * d2) / 2
Ejercicios resueltos
- Un
rombo tiene un lado de longitud 6 cm y una diagonal de 10 cm. Calcula su
perímetro y área.
Para calcular el perímetro, sumamos la longitud de los
cuatro lados:
Perímetro = 4 * 6 = 24 cm
Para calcular el área, multiplicamos las dos diagonales y dividimos el resultado por 2:
Área = (6 cm * 10 cm) / 2 = 30 cm2
Por lo tanto, el perímetro del rombo es de 24 cm y su área
es de 30 cm^2.
- La
diagonal de un rombo mide 16 cm y el ángulo que forma con uno de los lados
es de 30 grados. Calcula su perímetro y área.
Primero, podemos calcular la longitud de un lado del rombo
utilizando trigonometría:
cos(30°) = adyacente / hipotenusa
cos(30°) = a / (16 / 2)
a = (16 / 2) * cos(30°)
a = 6.93 cm (aproximadamente)
Para calcular el perímetro, multiplicamos la longitud de un
lado por 4:
Perímetro = 4 * 6.93 cm = 27.72 cm
Para calcular el área, podemos utilizar la fórmula del área
en función de las diagonales:
Área = (d1 * d2) / 2
Pero como el rombo es equidiagonal, d1 = d2 = 16 cm.
Entonces:
Área = (16 cm * 16 cm) / 2 = 128 cm2
Por lo tanto, el perímetro del rombo es de 27.72 cm y su área es de 128 cm2