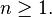9.4.23

Ecuacion de la circunferencia

By  Didacticol   5:17   , ,  

La Ecuación de la Circunferencia - Ejercicios Resueltos


La ecuación de la forma estándar de una círcunferencia es una forma de expresar la definición de de ésta en el plano de coordenadas.


• En el plano de coordenadas, la fórmula se convierte en:
(x-h)2 + (y-k)2 = r2
donde h y k son las coordenadas x e y del centro del círculo
o (x-9)2 + (y-6)2 = 100 es un círculo centrado en (9,6) con un radio de 10

Introducción a la Circunferencia

La circunferencia es una figura geométrica comúnmente vista en problemas de geometría y trigonometría. 

Se define como el conjunto de puntos en un plano que se encuentran a una distancia fija (llamada radio) de un punto fijo (llamado centro). La ecuación de la circunferencia es una forma de expresar la relación matemática entre los puntos de la circunferencia y su centro.

Ecuación de la circunferencia

La ecuación de la circunferencia se escribe en la forma estándar:

(x - h)2 + (y - k)2 = r2

donde (h, k) son las coordenadas del centro de la circunferencia y r es su radio.

Ejercicio Resuelto 1

Encuentre la ecuación de la circunferencia con centro en el punto (3, -2) y radio de 5 unidades.

Para resolver este problema, sustituimos los valores dados en la ecuación estándar de la circunferencia:

(x - 3)2 + (y + 2)2 = 25

Ejercicio Resuelto 2

Encuentre el centro y el radio de la circunferencia con la ecuación:

X2 + y2 - 4x + 6y + 9 = 0

Primero reorganizamos la ecuación para obtener la forma estándar de la ecuación de la circunferencia. 

Para hacer esto, agrupamos los términos que contienen x y y, y luego completamos el cuadrado para cada término:

(x2 - 4x) + (y2 + 6y) = -9

(x - 2)2 - 4 + (y + 3)2 - 9 = -9

(x - 2)2 + (y + 3)2 = 4

Por lo tanto, el centro de la circunferencia es (2, -3) y su radio es 2 unidades.

Conclusión sobre la ecuación de la circunferencia

La ecuación de la circunferencia es una herramienta útil en la geometría y la trigonometría, ya que nos permite describir la relación matemática entre los puntos de la circunferencia y su centro. 

Con la práctica, es fácil usar esta ecuación para resolver problemas de circunferencias en una variedad de contextos.


Leer más...

Teoria de Conjuntos Ejercicios Resueltos

By  Didacticol   4:48   , , ,  

Teoría de Conjuntos. Ejercicios

La teoría de conjuntos es la rama de las matemáticas que estudia los conjuntos, que son colecciones de objetos. 

Aunque cualquier tipo de objeto se puede recoger en un conjunto, la teoría de conjuntos se aplica con mayor frecuencia a los objetos que son relevantes para las matemáticas. 

El lenguaje de la teoría de conjuntos puede ser utilizado en las definiciones de casi todos los objetos matemáticos.

La Teoría de Conjuntos: Fundamento de las Matemáticas

El estudio moderno de la teoría de conjuntos fue iniciada por Georg Cantor y Dedekind Richard en 1870. 

Después del descubrimiento de las paradojas de la teoría de conjuntos, numerosos sistemas axiomáticos se propusieron en el siglo XX, de los cuales los axiomas de Zermelo-Fraenkel con el axioma de elección, son los más conocidos.

La teoría de conjuntos se refiere a la noción de un conjunto, esencialmente una colección de objetos que llamamos elementos.

Debido a su generalidad, la teoría de conjuntos es la base de casi todas las demás partes de las matemáticas.

Todas las matemáticas se basan en conjuntos

La teoría de conjuntos se emplea comúnmente como un sistema fundamental para las matemáticas, particularmente en la forma de la teoría de conjuntos de Zermelo-Fraenkel con el axioma de elección. 

Más allá de su papel fundacional, la teoría de conjuntos es una rama de las matemáticas en sí misma, con una comunidad de investigación activa. 

La investigación contemporánea en la teoría de conjuntos incluye una colección diversa de temas, que van desde la estructura de la recta numérica real para el estudio de la consistencia de los grandes cardinales.

Conceptos básicos de la teoría de conjuntos

Ejercicios Resueltos

La teoría de conjuntos se inicia con una relación binaria fundamental entre un objeto o y un conjunto A. Si o es un miembro (o elemento) de A, o ∈ A. Puesto que los conjuntos son objetos, la relación de pertenencia se puede relacionar con conjuntos también.

La Unión de los conjuntos A y B, se denotado A ∪ B, es el conjunto de todos los objetos que son miembros de A, o B, o ambos. La unión de {1, 2, 3} y
{ 3, 4} es el conjunto {1, 2, 3, 4}.

La Intersección de los conjuntos A y B, denotada A ∩ B, es el conjunto de todos los objetos que son miembros de A y B. La intersección de {1, 2, 3} y {2, 3, 4} es el conjunto {2, 3}.

Diferencia simétrica de los conjuntos A y B, denotado A △ B o A ⊖ B,
ejemplo, para los conjuntos {1,2,3} y {2,3,4}, el conjunto diferencia simétrica es {1,4}. Es la diferencia de conjuntos de la unión y la intersección, (A ∪ B) \ (A ∩ B) o (A \ B) ∪ (B \ A).

Producto cartesiano de A y B, denotada A × B, es el conjunto cuyos miembros son todos los posibles pares ordenados (a, b). El producto cartesiano de {1, 2} y {rojo, blanco} es {(1, rojo), (1, blanco), (2, rojo), (2, blanco)}.

El Conjunto potencia de un conjunto A es el conjunto cuyos miembros son todos los posibles subconjuntos de A. Por ejemplo, el conjunto potencia de {1, 2} es {{}, {1}, {2}, {1,2}}.





Leer más...

8.4.23

Ecuacion de la parabola ejercicios resueltos

By  Didacticol   8:48   , ,  

La Ecuación de la Parábola

En el área de matemáticas, una parábola es una sección cónica, creado a partir de la intersección de una superficie cónica circular derecha y un plano paralelo a una generatriz recta de la superficie. 

Parábolas: Definición y Cómo Encontrar su Ecuación a Partir del Foco y la Directriz

Otra manera de generar una parábola es examinar un punto (el foco) y una línea (la directriz). El lugar geométrico de todos los puntos en ese plano que son equidistantes de la línea es una parábola. 

En álgebra, las parábolas se encuentran con frecuencia en forma de gráficos de funciones cuadráticas.


               Ecuacion de la parabola ejercicios resueltos


Partes de una Parábola

La línea perpendicular a la directriz que pasa por el foco (es decir, la línea que divide la parábola a través de la parte central) se llama el "eje de simetría". 

El punto en el eje de simetría que se cruza con la parábola se llama el "vértice", y es el punto donde la curvatura es mayor. 

Longitud focal y dirección de apertura en parábolas

La distancia entre el vértice y el foco, medida a lo largo del eje de simetría, es la "longitud focal". Las parábolas puede abrir hacia arriba, abajo, izquierda, derecha, o en alguna dirección arbitraria.

Introducción sobre la ecuación de la parábola

La parábola es una de las secciones cónicas más comunes en matemáticas 

Es la curva que resulta de cortar un cono de revolución con un plano que forma un ángulo igual al de la generatriz con el eje del cono. 

La ecuación de la parábola es una de las formas más comunes para representarla en el plano cartesiano.

Ecuación de la parábola

La ecuación general de una parábola con vértice en el origen de coordenadas es:

Y2 = 4px

Donde p es la distancia entre el foco y el vértice de la parábola. Si la parábola está orientada hacia la derecha, la ecuación se escribe en términos de la coordenada x en lugar de y:

X2 = 4py

La ecuación de la parábola también se puede expresar en términos de su forma factorizada:

y = a(x - h)2 + k

Donde a, h y k son constantes y (h, k) es el vértice de la parábola. La constante a determina si la parábola se abre hacia arriba o hacia abajo.

Si a > 0, la parábola se abre hacia arriba, mientras que si a < 0, la parábola se abre hacia abajo.

Propiedades de la parábola

La parábola tiene varias propiedades

Estas se pueden utilizar para determinar sus características, como la dirección de apertura, el vértice, el foco y la directriz. 

Algunas de estas propiedades incluyen:

  • La distancia del foco al vértice de la parábola es igual a p, que es la distancia desde el vértice a la directriz de la parábola.
  • La ecuación de la directriz de la parábola es y = -p si la parábola se abre hacia arriba o hacia abajo, y x = -p si la parábola se abre hacia la derecha o hacia la izquierda.
  • El vértice de la parábola es el punto (h, k), donde h es la coordenada x del vértice y k es la coordenada y.
  • La distancia entre el vértice y el foco es la misma que la distancia entre el vértice y la directriz.
  • Si la parábola está orientada hacia arriba o hacia abajo, el eje de simetría es una línea vertical que pasa por el vértice de la parábola. Si la parábola está orientada hacia la izquierda o hacia la derecha, el eje de simetría es una línea horizontal que pasa por el vértice.

Ejemplos de problemas resueltos

A continuación, se presentan algunos ejemplos de problemas que se pueden resolver utilizando la ecuación de la parábola:

Ejemplo 1

Encuentra la ecuación de la parábola con vértice en (2,3) y foco en (2,5).

Solución: El vértice de la parábola es (h,k) = (2,3), por lo que la ecuación de la parábola tiene la forma:

(y - 3)2 = 4p(x - 2) Como el foco se encuentra en (2,5), sabemos que p = 1/4 (la distancia del vértice al foco es la misma que la distancia del vértice al punto de la parábola más cercano al eje de simetría, que es la distancia p).

Sustituyendo p en la ecuación de la parábola, obtenemos:

(y - 3)2 = (x - 2)

Lo que nos da la ecuación de la parábola en su forma canónica.

Ahora podemos encontrar la ecuación en su forma general despejando la variable y:

Y2 - 6y + 9 = x - 2

Moviendo los términos a la izquierda y simplificando, tenemos:

x = y2 - 6y + 11

Esta es la ecuación de la parábola en su forma general.

Ejemplo 2 

Encuentra la ecuación de la parábola con vértice en (0,0) y que pasa por el punto (2,8).

Solución: Como el vértice es el punto (h,k) = (0,0), la ecuación de la parábola tiene la forma:

Y2 = 4px

Donde p es la distancia del vértice al foco y al punto más cercano de la parábola al eje de simetría. Como no se nos da el valor de p, debemos encontrarlo usando la información adicional que nos proporciona el punto (2,8).

Primero, encontramos la coordenada x del punto de la parábola más cercano al eje de simetría. Como el vértice está en el origen, el punto más cercano al eje de simetría está en x = 0. Sustituyendo x = 0 en la ecuación de la parábola, obtenemos:

Y2 = 0

Por lo que y = 0 es el punto más cercano al eje de simetría.

Ahora podemos encontrar p utilizando la distancia entre el punto (2,8) y el punto más cercano al eje de simetría, que es:

p = (2 - 0)/4 = 1/2

Sustituyendo p en la ecuación de la parábola, obtenemos:

Y2 = 2x

Esta es la ecuación de la parábola en su forma canónica.

Para encontrar la ecuación en su forma general, podemos despejar la variable x:

x = y2/2

Esta es la ecuación de la parábola en su forma general.



Leer más...

7.4.23

La Media Aritmetica Ejercicios

By  Didacticol   9:34   , ,  

La media aritmética

Ejercicios resueltos de media aritmetica
Es una representación matemática del valor típico de una serie de números, calculada como la suma de todos los números de la serie dividido por el recuento de todos los números de la misma Serie.

La media aritmética se conoce comúnmente como "promedio"

En otras palabras la media aritmética de un conjunto de datos se obtiene tomando la suma de los datos, y luego dividiendo la suma por el número total de valores en el conjunto. Esto es lo que se conoce como un promedio.

Por ejemplo, si usted quiere el promedio de 10, 20, y 27, primero debe sumarlos para obtener 57. Luego divida por 3, ya que tenemos tres valores, y tenemos una media aritmética (promedio) de 19.

Características de la Media Aritmética

  1. La media aritmética es una medida de tendencia central que se utiliza para representar un conjunto de datos en un solo número.
  2. Se calcula sumando todos los valores del conjunto de datos y dividiendo el resultado entre el número de valores.
  3. La media aritmética es sensible a valores extremos o atípicos en el conjunto de datos, lo que puede afectar su valor.
  4. Si los datos están distribuidos de manera uniforme, la media aritmética es una buena representación del conjunto de datos.
  5. Si los datos están sesgados, la media aritmética puede no ser una buena medida de tendencia central y otras medidas, como la mediana o la moda, pueden ser más adecuadas.
  6. La media aritmética puede ser utilizada para comparar conjuntos de datos y hacer inferencias sobre la población a partir de muestras.
  7. Si los datos tienen unidades de medida, la media aritmética también tendrá esas unidades y puede ser interpretada como una cantidad promedio en esa escala.
  8. La media aritmética tiene propiedades algebraicas útiles, como la propiedad distributiva, que la hace útil en cálculos matemáticos y estadísticos.

Ejercicios Resueltos

  1. Encuentra la media aritmética de los siguientes números: 4, 8, 12, 16, 20. 
    Solución: La media aritmética se obtiene sumando todos los números y dividiendo entre la cantidad de números. Así: (4 + 8 + 12 + 16 + 20) / 5 = 12.
  2. Si la media aritmética de tres números es 10 y dos de ellos son 4 y 12, ¿cuál es el tercer número? 
    Solución: Primero, sumamos los dos números conocidos: 4 + 12 = 16. Luego, multiplicamos la media aritmética por la cantidad de números (3): 10 x 3 = 30. Finalmente, restamos la suma de los números conocidos al total: 30 - 16 = 14. Por lo tanto, el tercer número es 14.
  3. La media aritmética de cuatro números es 20. Si uno de los números es 30, ¿cuál es la media aritmética de los otros tres números? 
    Solución: Primero, sumamos los cuatro números: 4 x 20 = 80. Luego, restamos el número conocido (30): 80 - 30 = 50. Ahora dividimos entre la cantidad de números restantes (3): 50 / 3 = 16.67. Por lo tanto, la media aritmética de los otros tres números es 16.67.
  4. Si la media aritmética de dos números es 15 y uno de ellos es 9, ¿cuál es el otro número? 
    Solución: Primero, multiplicamos la media aritmética por la cantidad de números (2): 15 x 2 = 30. Luego, restamos el número conocido (9): 30 - 9 = 21. Por lo tanto, el otro número es 21.
  5. La media aritmética de cinco números es 12. Si uno de los números es 20, ¿cuál es la media aritmética de los otros cuatro números? 
    Solución: Primero, sumamos los cinco números: 5 x 12 = 60. Luego, restamos el número conocido (20): 60 - 20 = 40. Ahora dividimos entre la cantidad de números restantes (4): 40 / 4 = 10. Por lo tanto, la media aritmética de los otros cuatro números es 10.
  6. Si la media aritmética de tres números es 6 y uno de ellos es 3, ¿cuál es la media aritmética de los otros dos números? 
    Solución: Primero, multiplicamos la media aritmética por la cantidad de números (3): 6 x 3 = 18. Luego, restamos el número conocido (3): 18 - 3 = 15. Ahora dividimos entre la cantidad de números restantes (2): 15 / 2 = 7.5. Por lo tanto, la media aritmética de los otros dos números es 7.5.

Leer más...

DISTRIBUCION BINOMIAL - Ejercicios Resueltos

By  Didacticol   9:16   , ,  

Ejercicios de Distribución Binomial

Distribución binomial

La distribución binomial es una distribución de probabilidad discreta que describe el número de veces que ocurre un evento en una cantidaddeterminada de ensayos independientes y aleatorios, en los que el evento de interés tiene una probabilidad fija de ocurrencia en cada ensayo.

La distribución binomial se describe por dos parámetros: n, el número de ensayos, y p, la probabilidad de éxito en cada ensayo. Se representa matemáticamente como B(n, p).

Fórmula de la distribución binomial

La fórmula para la distribución binomial es:

P(X = k) = (nCk) * pk  * (1-p)(n-k)

donde:

  • P(X = k) es la probabilidad de que ocurra el evento de interés exactamente k veces en n ensayos independientes
  • nCk representa el coeficiente binomial, que es la cantidad de formas en que se pueden seleccionar k objetos de un conjunto de n objetos sin importar el orden
  • p es la probabilidad de éxito en cada ensayo
  • (1-p) es la probabilidad de fracaso en cada ensayo

Algunos aspectos importantes de la distribución binomial son:

  • Es una distribución de probabilidad discreta, ya que los resultados posibles son valores enteros y limitados.
  • La suma de todas las probabilidades posibles debe ser igual a 1.
  • La media de la distribución binomial es igual a n*p.
  • La varianza de la distribución binomial es igual a np(1-p).

 

Principales características de la distribución binomial

  1. La distribución binomial es un modelo de probabilidad discreta que se utiliza para describir eventos que solo pueden tener dos resultados posibles, como éxito o fracaso.
Leer más...

EJERCICIOS DE MULTIPLICACIÓN DE MATRICES

By  Didacticol   7:57   , ,  

EJERCICIOS DE MULTIPLICACIÓN DE MATRICES

Como multiplicar dos matrices

La multiplicación de matrices se divide en dos categorías generales:

Por un escalar en los que un número se multiplica con cada entrada de una matriz.

Multiplicación de toda una matriz por otra matriz entera, la multiplicación de matrices en ésta entrada se referirá a esta segunda categoría.

¿Qué es la multiplicación de la matriz?

Usted puede multiplicar dos matrices si, y sólo si, el número de columnas de la primera matriz es igual al número de filas de la segunda matriz.

De lo contrario, el producto de dos matrices no está definido.
Las dimensiones de la matriz producto son:

 (filas de la primera matriz) × (columnas de la segunda matriz)

EJERCICIO RESUELTO


\begin{pmatrix} 2 &0 \\ 4 &6 \\ 8 &2 \end{pmatrix} \begin{pmatrix} 1 &3 \\ 5 &7 \end{pmatrix} = \begin{pmatrix} 2\cdot 1+0\cdot 5 &2\cdot 3+0\cdot 7 \\ 4\cdot 1+6\cdot 5 &4\cdot 3+6\cdot 7 \\ 8\cdot 1+2\cdot 5 &8\cdot 3+2\cdot 7 \end{pmatrix} = \begin{pmatrix} 2 &6 \\ 34 &54 \\ 18 &38 \end{pmatrix}

La multiplicación de matrices casi nunca es conmutativa. Veamos que pasa al multiplicar matrices en ambos sentidos.


\begin{pmatrix} 1 &2 \\ 3 &4 \end{pmatrix} \begin{pmatrix} 5 &6 \\ 7 &8 \end{pmatrix} = \begin{pmatrix} 19 &22 \\ 43 &50 \end{pmatrix} \qquad \begin{pmatrix} 5 &6 \\ 7 &8 \end{pmatrix} \begin{pmatrix} 1 &2 \\ 3 &4 \end{pmatrix} = \begin{pmatrix} 23 &34 \\ 31 &46 \end{pmatrix}

EJERCICIOS RESUELTOS EN VÍDEO

Introducción: podemos estudiar los conceptos preliminares sobre las matrices y su orden; esto nos permitirá manejar de forma adecuada los conceptos básicos.

Cómo multiplicar matrices

Una matriz es un arreglo rectangular de números, símbolos o expresiones en filas y columnas. Para multiplicar matrices, tendrá que multiplicar los elementos (o números) de la fila de la primera matriz por los elementos de las filas de la segunda matriz. Puede multiplicar matrices en tan sólo unos sencillos pasos que veremos a continuación en el siguiente vídeo.

En términos generales tenemos que la multiplicación de dos matrices no es conmutativa, esto es:

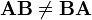
\mathbf{A}\mathbf{B} \neq \mathbf{B}\mathbf{A}

EJERCICIO DE MULTIPLICACIÓN DE MATRICES


\begin{align} \begin{pmatrix} {\color{Brown}1} & {\color{Orange}2} & {\color{Violet}3} \\ {\color{Brown}4} & {\color{Orange}5} & {\color{Violet}6} \\ {\color{Brown}7} & {\color{Orange}8} & {\color{Violet}9} \\ \end{pmatrix} \begin{pmatrix} {\color{Brown}a} & {\color{Brown}d} \\ {\color{Orange}b} & {\color{Orange}e} \\ {\color{Violet}c} & {\color{Violet}f} \\ \end{pmatrix} &= \begin{pmatrix} {\color{Brown}1} \\ {\color{Brown}4} \\ {\color{Brown}7} \\ \end{pmatrix} \begin{pmatrix} {\color{Brown}{a}} & {\color{Brown}{d}} \\ \end{pmatrix} + \begin{pmatrix} {\color{Orange}2} \\ {\color{Orange}5} \\ {\color{Orange}8}\\ \end{pmatrix} \begin{pmatrix} {\color{Orange}{b}} & {\color{Orange}{e}} \\ \end{pmatrix}+ \begin{pmatrix} {\color{Violet}3} \\ {\color{Violet}6} \\ {\color{Violet}9} \\ \end{pmatrix} \begin{pmatrix} {\color{Violet}c} & {\color{Violet}f} \\ \end{pmatrix} \\&= \begin{pmatrix} {\color{Brown}{1a}} & {\color{Brown}{1d}} \\ {\color{Brown}{4a}} & {\color{Brown}{4d}} \\ {\color{Brown}{7a}} & {\color{Brown}{7d}} \\ \end{pmatrix}+ \begin{pmatrix} {\color{Orange}{2b}} & {\color{Orange}{2e}} \\ {\color{Orange}{5b}} & {\color{Orange}{5e}} \\ {\color{Orange}{8b}} & {\color{Orange}{8e}} \\ \end{pmatrix}+ \begin{pmatrix} {\color{Violet}{3c}} & {\color{Violet}{3f}} \\ {\color{Violet}{6c}} & {\color{Violet}{6f}} \\ {\color{Violet}{9c}} & {\color{Violet}{9f}} \\ \end{pmatrix} \\&= \begin{pmatrix} {\color{Brown}{1a}} + {\color{Orange}{2b}} + {\color{Violet}{3c}} & {\color{Brown}{1d}} + {\color{Orange}{2e}} + {\color{Violet}{3f}} \\ {\color{Brown}{4a}} + {\color{Orange}{5b}} + {\color{Violet}{6c}} & {\color{Brown}{4d}} + {\color{Orange}{5e}} + {\color{Violet}{6f}} \\ {\color{Brown}{7a}} + {\color{Orange}{8b}} + {\color{Violet}{9c}} & {\color{Brown}{7d}} + {\color{Orange}{8e}} + {\color{Violet}{9f}} \\ \end{pmatrix}. \end{align}

¿Qué es Matrix?

La multiplicación de matrices no cumple con la propiedad conmutativa. Al Multiplicar A x B y B x A,  se presentan resultados diferentes. La multiplicación de matrices es la operación más útil y más común que se encuentra en las aplicaciones de algunos campos profesionales como la química.

Una matriz es un arreglo de números en filas y columnas que puede ser cuadrada, a menudo rectangular. 

Se puede establecer las dimensiones como m x n, donde (m) se refieren al número de filas y (n) al número de columnas. Los valores individuales que constituyen una matriz son conocidos como sus elementos, generalmente contemplados en filas y columnas. 

Como hemos expresado, las matrices tienen una variedad de aplicaciones; por ejemplo en química, también en el ajuste de curvas y en la mecánica cuántica o la teoría de grupos y gráficos moleculares. 

En la multiplicación de la matriz AxB, el número de columnas de la matriz A debe ser igual al número de filas de la matriz B. La matriz producto resultante tendrá el mismo número de filas que la matriz A y el mismo número de columnas que B.

Matriz identidad multiplicativa

La matriz identidad multiplicativa es una matriz que podemos multiplicar por otra matriz y la matriz resultante será igual a la matriz original.

Propiedades de la multiplicación

1. Cuando trabajamos con matrices, la multiplicación no es conmutativa.

AB ≠ BA

2. la multiplicación de matrices es asociativa. No importa cómo se agrupen tres o más matrices, cuando estas se multiplican, el resultado no cambia.

A(BC) = (AB) C

3. La multiplicación de matrices es asociativa, esto es análogo a la multiplicación algebraica simple. La única diferencia es que se mantenga el orden de la multiplicación.

A(B+C) = AB + AC ≠ (B + C) A = BA + CA

4. Si es una matriz cuadrada, existe un elemento de identidad para la multiplicación de la matriz. Se llama I

IA = IA = A


Las Matrices son ampliamente utilizadas en aplicaciones de gráficos de geometría, física e informática. En muchas aplicaciones es necesario calcular la multiplicación de la matriz 3 x 3.

Características de las Matrices

  • Las matrices son un arreglo rectangular de elementos, dispuestos en filas y columnas.
  • Las matrices pueden ser de distintas dimensiones, es decir, pueden tener diferentes números de filas y columnas.
  • Las matrices pueden ser clasificadas según su forma. Una matriz es cuadrada si tiene el mismo número de filas y columnas, y es rectangular en caso contrario.
  • Las matrices pueden ser clasificadas según sus elementos. Una matriz es nula si todos sus elementos son cero, y es identidad si tiene unos en su diagonal principal y ceros en el resto de sus elementos.
  • Las operaciones básicas que se pueden realizar con matrices incluyen la suma y la multiplicación.
  • La suma de dos matrices se realiza sumando elemento por elemento.
  • La multiplicación de dos matrices se realiza multiplicando filas por columnas y sumando los productos resultantes.
  • Las matrices también se pueden multiplicar por un escalar, es decir, por un número.
  • Las matrices pueden ser transpuestas, es decir, cambiando filas por columnas y viceversa.
  • Las matrices pueden ser invertibles o no invertibles, según si existe o no una matriz inversa que al multiplicarse por la matriz original de como resultado la matriz identidad.
  • Las matrices tienen aplicaciones en distintas ramas de las matemáticas y en otros campos como la física, la informática y la economía.
Leer más...

EJERCICIOS RESUELTOS DE PROGRESION GEOMETRICA

By  Didacticol   6:16   , , ,  

EJERCICIOS DE PROGRESIÓN GEOMÉTRICA

Una progresión geométrica que es también conocida como una secuencia geométrica, es sencillamente una secuencia de números, donde cada término después del primero se encuentra multiplicando el anterior por un número fijo distinto de cero llamado la razón común. 

Ejemplo, la secuencia de 2, 8, 32, 128, ... es una progresión geométrica con razón común de 4. Del mismo modo 10, 5, 2.5, 1.25, ... es una secuencia geométrica con razón común 1/2.

Ejemplos de una secuencia geométrica se pueden establecer con una potencia:  rk de un número r fijo, como  2k y 5k

Forma general de una progresión geométrica

a,\ ar,\ ar^2,\ ar^3,\ ar^4,\ \ldots

donde r ≠ 0 es la razón común y a es un factor de escala, igual a valor de inicio de la secuencia.

El término enésimo de una progresión geométrica con un valor inicial y razón común r está dada por

a_n = a\,r^{n-1}.

 Tal secuencia geométrica también sigue la relación establecida como:

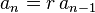 a_n = r\,a_{n-1}  donde n es un entero y  n\geq 1.

Generalmente, para comprobar si una secuencia dada es geométrico, uno simplemente comprueba si las entradas sucesivas en la secuencia de todas tienen la misma relación.

La razón común de una serie geométrica puede ser negativa, lo que resulta en una secuencia alterna, con los números de conmutación de positivo a negativo y viceversa. Por ejemplo:

1, -3, 9, -27, 81, -243, ...
es una secuencia geométrica con relación común de -3.

EJERCICIOS RESUELTOS DE PROGRESIÓN GEOMÉTRICA

Presentamos algunos problemas resueltos paso a paso para reforzar y afianzar los procedimientos. El vídeo muestra varios aspectos importantes.

El comportamiento de una secuencia geométrica depende del valor de la razón común.Si la relación común es:


  • Positiva, los términos serán todos del mismo signo que el término inicial.
  • Negativa, los términos se alternarán entre positivo y negativo.
  • Mayor que 1, habrá un crecimiento exponencial hacia el infinito positivo o negativo (según el signo del término inicial).
  • 1, la progresión es una secuencia constante.
  • Entre -1 y 1, pero no cero, habrá decaimiento exponencial a cero.
  • -1, La progresión es una secuencia alterna
  • Menos de -1, para los valores absolutos hay un crecimiento exponencial hacia (sin signo) el infinito, debido a la señal alterna.

PROBLEMAS RESUELTOS DE PROGRESIONES GEOMÉTRICAS

Un resultado interesante de la definición de una progresión geométrica es que para cualquier valor de la razón común, cualquiera de los tres aspectos consecutivos a, b y c tendrán que satisfacer la siguiente ecuación:


 b^2=ac

donde b se considera que es la media geométrica entre a y c.

EJERCICIOS RESUELTOS DE PROGRESIÓN ARITMÉTICA Y PROGRESIÓN GEOMÉTICA

Veamos en un mismo vídeo tanto la progresión aritmética como la progresión geométrica y encontrar las semejanzas y las diferencias entre éstas dos secuencias.



Serie geométrica

Una serie geométrica es la suma de los números en una progresión geométrica. Por ejemplo:


 2 + 10 + 50 + 250 = 2 + 2 \times 5 + 2 \times 5^2 + 2 \times 5^3. \,

Si tenemos que el primer término (en este caso 2), m el número de términos (en este caso 4), y r sea la constante de que cada término se multiplica por conseguir la próxima cantidad (en este caso 5), la suma está dada por:


 \frac{a(1-r^m)}{1-r}

En el ejemplo anterior, si resolvemos con la fórmula planteada, tenemos que:


 2 + 10 + 50 + 250 = \frac{2(1-5^4)}{1-5} = \frac{-1248}{-4} = 312.
Leer más...

EJERCICIO DE UTILIDAD, INGRESO TOTAL Y COSTO TOTAL - Matemática para Administración y Economía

By  Didacticol   5:10   , , , , , , ,  

EJERCICIO DE UTILIDAD, INGRESO TOTAL Y COSTO TOTAL - Matemática para Administración y Economía.

Ejercicios resueltos de utilidad, ingreso y costo total

Podemos establecer que el beneficio total de una empresa se determina por la diferencia entre sus ingresos totales y sus costos totales.

Adicionalmente, los costos totales se calculan sumando los costos variables y los costos fijos.

Optimización de ganancias en empresas utilizando matemáticas financieras

Una empresa logra maximizar sus ganancias o beneficios totales a corto plazo en el punto en el cual se encuentra la mayor diferencia positiva entre sus ingresos totales y sus gastos totales.

Los ejercicios resueltos de utilidad, ingreso total y costo total, nos permiten tomar habilidades que nos permiten estudiar y dominar las matemáticas para administración y economía.

Es de gran importancia practicar problemas y ejercicios de administración y ejercicios de economía.

A continuación presentamos un problema para su planteamiento:

PROBLEMA Y EJERCICIO RESUELTO:

Una compañía fabrica un producto para el cual el costo variable por unidad es de $6 y el costo fijo de $80.000. Cada unidad tiene un precio de venta de $10. Determine el número de unidades que deben venderse para obtener una utilidad de $60.000.



Cómo una empresa puede obtener más ganancias en un mercado competitivo

Para una empresa competitiva la maximización de todas sus utilidades dependerá básicamente de los ingresos obtenidos por las unidades que ésta logre producir y vender al precio fijado por el mercado.  

A todo ésto se le debe restar los costos de producción y demás.

Debido a que la empresa en un mercado perfectamente competitivo no puede influir sobre el mercado limitando su producción para obtener un precio mayor. 

Tampoco puede reducir sus precios para aumentar sus ventas, no tiene más remedio que aceptar el precio del mercado.

Utilidad en la Empresa

Teniendo en cuenta lo anterior para maximizar sus utilidades la empresa trata de ajustar sus volúmenes de producción de tal forma que obtenga con el precio fijado por el mercado la máxima utilidad posible, teniendo en cuenta la estructura de costos que tenga.

INGRESOS: 

Los ingresos corrientes de una empresa cooperativa resultan de las ventas. 

En otras palabras, los ingresos son iguales a la cantidad vendida, multiplicada por el precio unitario y en el caso de una cooperativa de servicios financieros, el total de ingresos está representado por la suma total de los servicios prestados, multiplicados por la tarifa establecida. 

Sin embargo, esos cálculos fríos esconden las verdaderas razones del ingreso de una actividad económica, éstas dependen de dos comportamientos: el del consumidor y el del empresario. Seguidamente, se analiza cada uno de ellos.  

Los Costos Variables 

Son todos aquellos costos que mantienen una relación directa con las cantidades producidas y varían de manera proporcional, con el uso de la capacidad instalada. 

De esta manera, un costo variable típico consiste en el consumo de las materias primas directas.


Leer más...

FUNCIONES TRIGONOMETRICAS

By  Didacticol   5:00   , ,  

Las Funciones Trigonométricas

Introducción:

Las funciones trigonométricas son un conjunto de funciones matemáticas que se utilizan para describir y modelar fenómenos periódicos, como el movimiento oscilatorio, las ondas sonoras y electromagnéticas, entre otros. 

En este artículo, exploraremos las seis funciones trigonométricas básicas: seno, coseno, tangente, cotangente, secante y cosecante. Además, sus aplicaciones en la resolución de problemas y situaciones prácticas.

Las seis funciones trigonométricas

  1. Definiciones y características de las funciones trigonométricas

  • El seno (sin) es la relación entre el cateto opuesto y la hipotenusa de un triángulo rectángulo.
  • El coseno (cos) es la relación entre el cateto adyacente y la hipotenusa de un triángulo rectángulo.
  • La tangente (tan) es la relación entre el cateto opuesto y el cateto adyacente de un triángulo rectángulo.
  • La cotangente (cot) es la relación entre el cateto adyacente y el cateto opuesto de un triángulo rectángulo.
  • La secante (sec) es la inversa del coseno y es la relación entre la hipotenusa y el cateto adyacente de un triángulo rectángulo.
  • La cosecante (csc) es la inversa del seno y es la relación entre la hipotenusa y el cateto opuesto de un triángulo rectángulo.

  1. Propiedades de las funciones trigonométricas

  • Las funciones seno y coseno son funciones periódicas con un período de 2π.
  • La función tangente tiene asíntotas en los ángulos de π/2 y 3π/2.
  • La función cotangente tiene asíntotas en los ángulos de 0 y π.
  • La función secante tiene asíntotas en los ángulos de π/2 y 3π/2.
  • La función cosecante tiene asíntotas en los ángulos de 0 y π.

Aplicaciones de las funciones trigonométricas

  1. Resolución de triángulos
  • Las funciones trigonométricas se utilizan para resolver triángulos rectángulos y no rectángulos a través de la ley de senos y la ley de cosenos.
  1. Modelado de fenómenos periódicos
  • Las funciones trigonométricas se utilizan para modelar fenómenos periódicos, como el movimiento oscilatorio, las ondas sonoras y electromagnéticas, entre otros.
  1. Problemas de física y geometría
  • Las funciones trigonométricas se utilizan en la resolución de problemas de física y geometría, como la determinación de la altura de un edificio o la trayectoria de un proyectil.
  1. Aplicaciones en la ingeniería y la tecnología
  • Las funciones trigonométricas se utilizan en la ingeniería y la tecnología, como en el diseño de puentes y edificios, la medición de la altura de un objeto, la creación de gráficos y animaciones en computadora, entre otros.

Ejemplos de problemas resueltos

Hallar la medida de los ángulos de un triángulo rectángulo si se conoce la longitud de sus lados.

Solución:

Supongamos que los lados del triángulo rectángulo son a, b y c, donde c es la hipotenusa y los ángulos opuestos a los lados a, b y c son A, B y C respectivamente. Entonces, por el teorema de Pitágoras, tenemos:

c2 = a2 + b2

Además, sabemos que el ángulo opuesto al lado a es A, el ángulo opuesto al lado b es B y el ángulo opuesto al lado c es C. Por lo tanto, tenemos las siguientes relaciones trigonométricas:

sen A = a/c

cos A = b/c

tan A = a/b

sen B = b/c

cos B = a/c

tan B = b/a

Por lo tanto, podemos hallar los ángulos A y B en función de las longitudes de los lados del triángulo:

sen A = a/c

A = arcsen(a/c)

sen B = b/c

B = arcsen(b/c)

Y, por último, podemos hallar el ángulo C sumando los ángulos A y B y restando el resultado de 180 grados:

C = 180 - A - B

Ejemplo:

Supongamos que tenemos un triángulo rectángulo con lados de longitud a = 3 y b = 4. Queremos hallar la medida de sus ángulos.

Primero, podemos hallar la longitud de la hipotenusa c usando el teorema de Pitágoras:

c2 = a2 + b2 = 32 + 42 = 9 + 16 = 25

c = √ (25) = 5

Luego, podemos hallar los ángulos A y B:

sen A = a/c = 3/5

A = arcsen(3/5) = 36.87 grados

sen B = b/c = 4/5

B = arcsen(4/5) = 53.13 grados

Por último, podemos hallar el ángulo C:

C = 180 - A - B = 180 - 36.87 - 53.13 = 90 grados

Por lo tanto, el triángulo rectángulo tiene ángulos de medida 36.87 grados, 53.13 grados y 90 grados.

¿Por qué aprender acerca de las funciones trigonométricas?

Las funciones trigonométricas son muy importantes en temas técnicos como la ciencia, la ingeniería, la arquitectura, e incluso la medicina. Usted se encontrará con ellos todo el tiempo, así que vale la pena aprenderlas de forma adecuada.

La Topografía es un área de aplicaciones de la trigonometria. Los fabricantes de carreteras, constructores de puentes y aquellos cuyo trabajo consiste en construir aplican de manera profunda ésta área de las matemáticas, la cual usan en su trabajo.




En matemáticas, las funciones trigonométricas (también llamados las funciones circulares) son funciones correspondientes a un ángulo. Ellas se utilizan para relacionar los ángulos de un triángulo y las longitudes de los lados de ese mismo triángulo. Las funciones trigonométricas son importantes en el estudio de los triángulos y los fenómenos que tienen modelos periódicos, entre otras muchas aplicaciones.





Leer más...