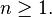Menú

▼

PÁGINAS

▼

7.4.23

La Media Aritmetica Ejercicios

La media aritmética

Ejercicios resueltos de media aritmetica
Es una representación matemática del valor típico de una serie de números, calculada como la suma de todos los números de la serie dividido por el recuento de todos los números de la misma Serie.

La media aritmética se conoce comúnmente como "promedio"

En otras palabras la media aritmética de un conjunto de datos se obtiene tomando la suma de los datos, y luego dividiendo la suma por el número total de valores en el conjunto. Esto es lo que se conoce como un promedio.

Por ejemplo, si usted quiere el promedio de 10, 20, y 27, primero debe sumarlos para obtener 57. Luego divida por 3, ya que tenemos tres valores, y tenemos una media aritmética (promedio) de 19.

Características de la Media Aritmética

  1. La media aritmética es una medida de tendencia central que se utiliza para representar un conjunto de datos en un solo número.
  2. Se calcula sumando todos los valores del conjunto de datos y dividiendo el resultado entre el número de valores.
  3. La media aritmética es sensible a valores extremos o atípicos en el conjunto de datos, lo que puede afectar su valor.
  4. Si los datos están distribuidos de manera uniforme, la media aritmética es una buena representación del conjunto de datos.
  5. Si los datos están sesgados, la media aritmética puede no ser una buena medida de tendencia central y otras medidas, como la mediana o la moda, pueden ser más adecuadas.
  6. La media aritmética puede ser utilizada para comparar conjuntos de datos y hacer inferencias sobre la población a partir de muestras.
  7. Si los datos tienen unidades de medida, la media aritmética también tendrá esas unidades y puede ser interpretada como una cantidad promedio en esa escala.
  8. La media aritmética tiene propiedades algebraicas útiles, como la propiedad distributiva, que la hace útil en cálculos matemáticos y estadísticos.

Ejercicios Resueltos

  1. Encuentra la media aritmética de los siguientes números: 4, 8, 12, 16, 20. 
    Solución: La media aritmética se obtiene sumando todos los números y dividiendo entre la cantidad de números. Así: (4 + 8 + 12 + 16 + 20) / 5 = 12.
  2. Si la media aritmética de tres números es 10 y dos de ellos son 4 y 12, ¿cuál es el tercer número? 
    Solución: Primero, sumamos los dos números conocidos: 4 + 12 = 16. Luego, multiplicamos la media aritmética por la cantidad de números (3): 10 x 3 = 30. Finalmente, restamos la suma de los números conocidos al total: 30 - 16 = 14. Por lo tanto, el tercer número es 14.
  3. La media aritmética de cuatro números es 20. Si uno de los números es 30, ¿cuál es la media aritmética de los otros tres números? 
    Solución: Primero, sumamos los cuatro números: 4 x 20 = 80. Luego, restamos el número conocido (30): 80 - 30 = 50. Ahora dividimos entre la cantidad de números restantes (3): 50 / 3 = 16.67. Por lo tanto, la media aritmética de los otros tres números es 16.67.
  4. Si la media aritmética de dos números es 15 y uno de ellos es 9, ¿cuál es el otro número? 
    Solución: Primero, multiplicamos la media aritmética por la cantidad de números (2): 15 x 2 = 30. Luego, restamos el número conocido (9): 30 - 9 = 21. Por lo tanto, el otro número es 21.
  5. La media aritmética de cinco números es 12. Si uno de los números es 20, ¿cuál es la media aritmética de los otros cuatro números? 
    Solución: Primero, sumamos los cinco números: 5 x 12 = 60. Luego, restamos el número conocido (20): 60 - 20 = 40. Ahora dividimos entre la cantidad de números restantes (4): 40 / 4 = 10. Por lo tanto, la media aritmética de los otros cuatro números es 10.
  6. Si la media aritmética de tres números es 6 y uno de ellos es 3, ¿cuál es la media aritmética de los otros dos números? 
    Solución: Primero, multiplicamos la media aritmética por la cantidad de números (3): 6 x 3 = 18. Luego, restamos el número conocido (3): 18 - 3 = 15. Ahora dividimos entre la cantidad de números restantes (2): 15 / 2 = 7.5. Por lo tanto, la media aritmética de los otros dos números es 7.5.

DISTRIBUCION BINOMIAL - Ejercicios Resueltos

Ejercicios de Distribución Binomial

Distribución binomial

La distribución binomial es una distribución de probabilidad discreta que describe el número de veces que ocurre un evento en una cantidaddeterminada de ensayos independientes y aleatorios, en los que el evento de interés tiene una probabilidad fija de ocurrencia en cada ensayo.

La distribución binomial se describe por dos parámetros: n, el número de ensayos, y p, la probabilidad de éxito en cada ensayo. Se representa matemáticamente como B(n, p).

Fórmula de la distribución binomial

La fórmula para la distribución binomial es:

P(X = k) = (nCk) * pk  * (1-p)(n-k)

donde:

  • P(X = k) es la probabilidad de que ocurra el evento de interés exactamente k veces en n ensayos independientes
  • nCk representa el coeficiente binomial, que es la cantidad de formas en que se pueden seleccionar k objetos de un conjunto de n objetos sin importar el orden
  • p es la probabilidad de éxito en cada ensayo
  • (1-p) es la probabilidad de fracaso en cada ensayo

Algunos aspectos importantes de la distribución binomial son:

  • Es una distribución de probabilidad discreta, ya que los resultados posibles son valores enteros y limitados.
  • La suma de todas las probabilidades posibles debe ser igual a 1.
  • La media de la distribución binomial es igual a n*p.
  • La varianza de la distribución binomial es igual a np(1-p).

 

Principales características de la distribución binomial

  1. La distribución binomial es un modelo de probabilidad discreta que se utiliza para describir eventos que solo pueden tener dos resultados posibles, como éxito o fracaso.

EJERCICIOS DE MULTIPLICACIÓN DE MATRICES

EJERCICIOS DE MULTIPLICACIÓN DE MATRICES

Como multiplicar dos matrices

La multiplicación de matrices se divide en dos categorías generales:

Por un escalar en los que un número se multiplica con cada entrada de una matriz.

Multiplicación de toda una matriz por otra matriz entera, la multiplicación de matrices en ésta entrada se referirá a esta segunda categoría.

¿Qué es la multiplicación de la matriz?

Usted puede multiplicar dos matrices si, y sólo si, el número de columnas de la primera matriz es igual al número de filas de la segunda matriz.

De lo contrario, el producto de dos matrices no está definido.
Las dimensiones de la matriz producto son:

 (filas de la primera matriz) × (columnas de la segunda matriz)

EJERCICIO RESUELTO


\begin{pmatrix} 2 &0 \\ 4 &6 \\ 8 &2 \end{pmatrix} \begin{pmatrix} 1 &3 \\ 5 &7 \end{pmatrix} = \begin{pmatrix} 2\cdot 1+0\cdot 5 &2\cdot 3+0\cdot 7 \\ 4\cdot 1+6\cdot 5 &4\cdot 3+6\cdot 7 \\ 8\cdot 1+2\cdot 5 &8\cdot 3+2\cdot 7 \end{pmatrix} = \begin{pmatrix} 2 &6 \\ 34 &54 \\ 18 &38 \end{pmatrix}

La multiplicación de matrices casi nunca es conmutativa. Veamos que pasa al multiplicar matrices en ambos sentidos.


\begin{pmatrix} 1 &2 \\ 3 &4 \end{pmatrix} \begin{pmatrix} 5 &6 \\ 7 &8 \end{pmatrix} = \begin{pmatrix} 19 &22 \\ 43 &50 \end{pmatrix} \qquad \begin{pmatrix} 5 &6 \\ 7 &8 \end{pmatrix} \begin{pmatrix} 1 &2 \\ 3 &4 \end{pmatrix} = \begin{pmatrix} 23 &34 \\ 31 &46 \end{pmatrix}

EJERCICIOS RESUELTOS EN VÍDEO

Introducción: podemos estudiar los conceptos preliminares sobre las matrices y su orden; esto nos permitirá manejar de forma adecuada los conceptos básicos.

Cómo multiplicar matrices

Una matriz es un arreglo rectangular de números, símbolos o expresiones en filas y columnas. Para multiplicar matrices, tendrá que multiplicar los elementos (o números) de la fila de la primera matriz por los elementos de las filas de la segunda matriz. Puede multiplicar matrices en tan sólo unos sencillos pasos que veremos a continuación en el siguiente vídeo.

En términos generales tenemos que la multiplicación de dos matrices no es conmutativa, esto es:

\mathbf{A}\mathbf{B} \neq \mathbf{B}\mathbf{A}

EJERCICIO DE MULTIPLICACIÓN DE MATRICES


\begin{align} \begin{pmatrix} {\color{Brown}1} & {\color{Orange}2} & {\color{Violet}3} \\ {\color{Brown}4} & {\color{Orange}5} & {\color{Violet}6} \\ {\color{Brown}7} & {\color{Orange}8} & {\color{Violet}9} \\ \end{pmatrix} \begin{pmatrix} {\color{Brown}a} & {\color{Brown}d} \\ {\color{Orange}b} & {\color{Orange}e} \\ {\color{Violet}c} & {\color{Violet}f} \\ \end{pmatrix} &= \begin{pmatrix} {\color{Brown}1} \\ {\color{Brown}4} \\ {\color{Brown}7} \\ \end{pmatrix} \begin{pmatrix} {\color{Brown}{a}} & {\color{Brown}{d}} \\ \end{pmatrix} + \begin{pmatrix} {\color{Orange}2} \\ {\color{Orange}5} \\ {\color{Orange}8}\\ \end{pmatrix} \begin{pmatrix} {\color{Orange}{b}} & {\color{Orange}{e}} \\ \end{pmatrix}+ \begin{pmatrix} {\color{Violet}3} \\ {\color{Violet}6} \\ {\color{Violet}9} \\ \end{pmatrix} \begin{pmatrix} {\color{Violet}c} & {\color{Violet}f} \\ \end{pmatrix} \\&= \begin{pmatrix} {\color{Brown}{1a}} & {\color{Brown}{1d}} \\ {\color{Brown}{4a}} & {\color{Brown}{4d}} \\ {\color{Brown}{7a}} & {\color{Brown}{7d}} \\ \end{pmatrix}+ \begin{pmatrix} {\color{Orange}{2b}} & {\color{Orange}{2e}} \\ {\color{Orange}{5b}} & {\color{Orange}{5e}} \\ {\color{Orange}{8b}} & {\color{Orange}{8e}} \\ \end{pmatrix}+ \begin{pmatrix} {\color{Violet}{3c}} & {\color{Violet}{3f}} \\ {\color{Violet}{6c}} & {\color{Violet}{6f}} \\ {\color{Violet}{9c}} & {\color{Violet}{9f}} \\ \end{pmatrix} \\&= \begin{pmatrix} {\color{Brown}{1a}} + {\color{Orange}{2b}} + {\color{Violet}{3c}} & {\color{Brown}{1d}} + {\color{Orange}{2e}} + {\color{Violet}{3f}} \\ {\color{Brown}{4a}} + {\color{Orange}{5b}} + {\color{Violet}{6c}} & {\color{Brown}{4d}} + {\color{Orange}{5e}} + {\color{Violet}{6f}} \\ {\color{Brown}{7a}} + {\color{Orange}{8b}} + {\color{Violet}{9c}} & {\color{Brown}{7d}} + {\color{Orange}{8e}} + {\color{Violet}{9f}} \\ \end{pmatrix}. \end{align}

¿Qué es Matrix?

La multiplicación de matrices no cumple con la propiedad conmutativa. Al Multiplicar A x B y B x A,  se presentan resultados diferentes. La multiplicación de matrices es la operación más útil y más común que se encuentra en las aplicaciones de algunos campos profesionales como la química.

Una matriz es un arreglo de números en filas y columnas que puede ser cuadrada, a menudo rectangular. 

Se puede establecer las dimensiones como m x n, donde (m) se refieren al número de filas y (n) al número de columnas. Los valores individuales que constituyen una matriz son conocidos como sus elementos, generalmente contemplados en filas y columnas. 

Como hemos expresado, las matrices tienen una variedad de aplicaciones; por ejemplo en química, también en el ajuste de curvas y en la mecánica cuántica o la teoría de grupos y gráficos moleculares. 

En la multiplicación de la matriz AxB, el número de columnas de la matriz A debe ser igual al número de filas de la matriz B. La matriz producto resultante tendrá el mismo número de filas que la matriz A y el mismo número de columnas que B.

Matriz identidad multiplicativa

La matriz identidad multiplicativa es una matriz que podemos multiplicar por otra matriz y la matriz resultante será igual a la matriz original.

Propiedades de la multiplicación

1. Cuando trabajamos con matrices, la multiplicación no es conmutativa.

AB ≠ BA

2. la multiplicación de matrices es asociativa. No importa cómo se agrupen tres o más matrices, cuando estas se multiplican, el resultado no cambia.

A(BC) = (AB) C

3. La multiplicación de matrices es asociativa, esto es análogo a la multiplicación algebraica simple. La única diferencia es que se mantenga el orden de la multiplicación.

A(B+C) = AB + AC ≠ (B + C) A = BA + CA

4. Si es una matriz cuadrada, existe un elemento de identidad para la multiplicación de la matriz. Se llama I

IA = IA = A


Las Matrices son ampliamente utilizadas en aplicaciones de gráficos de geometría, física e informática. En muchas aplicaciones es necesario calcular la multiplicación de la matriz 3 x 3.

Características de las Matrices

  • Las matrices son un arreglo rectangular de elementos, dispuestos en filas y columnas.
  • Las matrices pueden ser de distintas dimensiones, es decir, pueden tener diferentes números de filas y columnas.
  • Las matrices pueden ser clasificadas según su forma. Una matriz es cuadrada si tiene el mismo número de filas y columnas, y es rectangular en caso contrario.
  • Las matrices pueden ser clasificadas según sus elementos. Una matriz es nula si todos sus elementos son cero, y es identidad si tiene unos en su diagonal principal y ceros en el resto de sus elementos.
  • Las operaciones básicas que se pueden realizar con matrices incluyen la suma y la multiplicación.
  • La suma de dos matrices se realiza sumando elemento por elemento.
  • La multiplicación de dos matrices se realiza multiplicando filas por columnas y sumando los productos resultantes.
  • Las matrices también se pueden multiplicar por un escalar, es decir, por un número.
  • Las matrices pueden ser transpuestas, es decir, cambiando filas por columnas y viceversa.
  • Las matrices pueden ser invertibles o no invertibles, según si existe o no una matriz inversa que al multiplicarse por la matriz original de como resultado la matriz identidad.
  • Las matrices tienen aplicaciones en distintas ramas de las matemáticas y en otros campos como la física, la informática y la economía.

EJERCICIOS RESUELTOS DE PROGRESION GEOMETRICA

EJERCICIOS DE PROGRESIÓN GEOMÉTRICA

Una progresión geométrica que es también conocida como una secuencia geométrica, es sencillamente una secuencia de números, donde cada término después del primero se encuentra multiplicando el anterior por un número fijo distinto de cero llamado la razón común. 

Ejemplo, la secuencia de 2, 8, 32, 128, ... es una progresión geométrica con razón común de 4. Del mismo modo 10, 5, 2.5, 1.25, ... es una secuencia geométrica con razón común 1/2.

Ejemplos de una secuencia geométrica se pueden establecer con una potencia:  rk de un número r fijo, como  2k y 5k

Forma general de una progresión geométrica

a,\ ar,\ ar^2,\ ar^3,\ ar^4,\ \ldots

donde r ≠ 0 es la razón común y a es un factor de escala, igual a valor de inicio de la secuencia.

El término enésimo de una progresión geométrica con un valor inicial y razón común r está dada por

a_n = a\,r^{n-1}.

 Tal secuencia geométrica también sigue la relación establecida como:

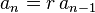 a_n = r\,a_{n-1}  donde n es un entero y  n\geq 1.

Generalmente, para comprobar si una secuencia dada es geométrico, uno simplemente comprueba si las entradas sucesivas en la secuencia de todas tienen la misma relación.

La razón común de una serie geométrica puede ser negativa, lo que resulta en una secuencia alterna, con los números de conmutación de positivo a negativo y viceversa. Por ejemplo:

1, -3, 9, -27, 81, -243, ...
es una secuencia geométrica con relación común de -3.

EJERCICIOS RESUELTOS DE PROGRESIÓN GEOMÉTRICA

Presentamos algunos problemas resueltos paso a paso para reforzar y afianzar los procedimientos. El vídeo muestra varios aspectos importantes.

El comportamiento de una secuencia geométrica depende del valor de la razón común.Si la relación común es:


  • Positiva, los términos serán todos del mismo signo que el término inicial.
  • Negativa, los términos se alternarán entre positivo y negativo.
  • Mayor que 1, habrá un crecimiento exponencial hacia el infinito positivo o negativo (según el signo del término inicial).
  • 1, la progresión es una secuencia constante.
  • Entre -1 y 1, pero no cero, habrá decaimiento exponencial a cero.
  • -1, La progresión es una secuencia alterna
  • Menos de -1, para los valores absolutos hay un crecimiento exponencial hacia (sin signo) el infinito, debido a la señal alterna.

PROBLEMAS RESUELTOS DE PROGRESIONES GEOMÉTRICAS

Un resultado interesante de la definición de una progresión geométrica es que para cualquier valor de la razón común, cualquiera de los tres aspectos consecutivos a, b y c tendrán que satisfacer la siguiente ecuación:


 b^2=ac

donde b se considera que es la media geométrica entre a y c.

EJERCICIOS RESUELTOS DE PROGRESIÓN ARITMÉTICA Y PROGRESIÓN GEOMÉTICA

Veamos en un mismo vídeo tanto la progresión aritmética como la progresión geométrica y encontrar las semejanzas y las diferencias entre éstas dos secuencias.



Serie geométrica

Una serie geométrica es la suma de los números en una progresión geométrica. Por ejemplo:


 2 + 10 + 50 + 250 = 2 + 2 \times 5 + 2 \times 5^2 + 2 \times 5^3. \,

Si tenemos que el primer término (en este caso 2), m el número de términos (en este caso 4), y r sea la constante de que cada término se multiplica por conseguir la próxima cantidad (en este caso 5), la suma está dada por:


 \frac{a(1-r^m)}{1-r}

En el ejemplo anterior, si resolvemos con la fórmula planteada, tenemos que:


 2 + 10 + 50 + 250 = \frac{2(1-5^4)}{1-5} = \frac{-1248}{-4} = 312.

EJERCICIO DE UTILIDAD, INGRESO TOTAL Y COSTO TOTAL - Matemática para Administración y Economía

EJERCICIO DE UTILIDAD, INGRESO TOTAL Y COSTO TOTAL - Matemática para Administración y Economía.

Ejercicios resueltos de utilidad, ingreso y costo total

Podemos establecer que el beneficio total de una empresa se determina por la diferencia entre sus ingresos totales y sus costos totales.

Adicionalmente, los costos totales se calculan sumando los costos variables y los costos fijos.

Optimización de ganancias en empresas utilizando matemáticas financieras

Una empresa logra maximizar sus ganancias o beneficios totales a corto plazo en el punto en el cual se encuentra la mayor diferencia positiva entre sus ingresos totales y sus gastos totales.

Los ejercicios resueltos de utilidad, ingreso total y costo total, nos permiten tomar habilidades que nos permiten estudiar y dominar las matemáticas para administración y economía.

Es de gran importancia practicar problemas y ejercicios de administración y ejercicios de economía.

A continuación presentamos un problema para su planteamiento:

PROBLEMA Y EJERCICIO RESUELTO:

Una compañía fabrica un producto para el cual el costo variable por unidad es de $6 y el costo fijo de $80.000. Cada unidad tiene un precio de venta de $10. Determine el número de unidades que deben venderse para obtener una utilidad de $60.000.



Cómo una empresa puede obtener más ganancias en un mercado competitivo

Para una empresa competitiva la maximización de todas sus utilidades dependerá básicamente de los ingresos obtenidos por las unidades que ésta logre producir y vender al precio fijado por el mercado.  

A todo ésto se le debe restar los costos de producción y demás.

Debido a que la empresa en un mercado perfectamente competitivo no puede influir sobre el mercado limitando su producción para obtener un precio mayor. 

Tampoco puede reducir sus precios para aumentar sus ventas, no tiene más remedio que aceptar el precio del mercado.

Utilidad en la Empresa

Teniendo en cuenta lo anterior para maximizar sus utilidades la empresa trata de ajustar sus volúmenes de producción de tal forma que obtenga con el precio fijado por el mercado la máxima utilidad posible, teniendo en cuenta la estructura de costos que tenga.

INGRESOS: 

Los ingresos corrientes de una empresa cooperativa resultan de las ventas. 

En otras palabras, los ingresos son iguales a la cantidad vendida, multiplicada por el precio unitario y en el caso de una cooperativa de servicios financieros, el total de ingresos está representado por la suma total de los servicios prestados, multiplicados por la tarifa establecida. 

Sin embargo, esos cálculos fríos esconden las verdaderas razones del ingreso de una actividad económica, éstas dependen de dos comportamientos: el del consumidor y el del empresario. Seguidamente, se analiza cada uno de ellos.  

Los Costos Variables 

Son todos aquellos costos que mantienen una relación directa con las cantidades producidas y varían de manera proporcional, con el uso de la capacidad instalada. 

De esta manera, un costo variable típico consiste en el consumo de las materias primas directas.


FUNCIONES TRIGONOMETRICAS

Las Funciones Trigonométricas

Introducción:

Las funciones trigonométricas son un conjunto de funciones matemáticas que se utilizan para describir y modelar fenómenos periódicos, como el movimiento oscilatorio, las ondas sonoras y electromagnéticas, entre otros. 

En este artículo, exploraremos las seis funciones trigonométricas básicas: seno, coseno, tangente, cotangente, secante y cosecante. Además, sus aplicaciones en la resolución de problemas y situaciones prácticas.

Las seis funciones trigonométricas

  1. Definiciones y características de las funciones trigonométricas

  • El seno (sin) es la relación entre el cateto opuesto y la hipotenusa de un triángulo rectángulo.
  • El coseno (cos) es la relación entre el cateto adyacente y la hipotenusa de un triángulo rectángulo.
  • La tangente (tan) es la relación entre el cateto opuesto y el cateto adyacente de un triángulo rectángulo.
  • La cotangente (cot) es la relación entre el cateto adyacente y el cateto opuesto de un triángulo rectángulo.
  • La secante (sec) es la inversa del coseno y es la relación entre la hipotenusa y el cateto adyacente de un triángulo rectángulo.
  • La cosecante (csc) es la inversa del seno y es la relación entre la hipotenusa y el cateto opuesto de un triángulo rectángulo.

  1. Propiedades de las funciones trigonométricas

  • Las funciones seno y coseno son funciones periódicas con un período de 2π.
  • La función tangente tiene asíntotas en los ángulos de π/2 y 3π/2.
  • La función cotangente tiene asíntotas en los ángulos de 0 y π.
  • La función secante tiene asíntotas en los ángulos de π/2 y 3π/2.
  • La función cosecante tiene asíntotas en los ángulos de 0 y π.

Aplicaciones de las funciones trigonométricas

  1. Resolución de triángulos
  • Las funciones trigonométricas se utilizan para resolver triángulos rectángulos y no rectángulos a través de la ley de senos y la ley de cosenos.
  1. Modelado de fenómenos periódicos
  • Las funciones trigonométricas se utilizan para modelar fenómenos periódicos, como el movimiento oscilatorio, las ondas sonoras y electromagnéticas, entre otros.
  1. Problemas de física y geometría
  • Las funciones trigonométricas se utilizan en la resolución de problemas de física y geometría, como la determinación de la altura de un edificio o la trayectoria de un proyectil.
  1. Aplicaciones en la ingeniería y la tecnología
  • Las funciones trigonométricas se utilizan en la ingeniería y la tecnología, como en el diseño de puentes y edificios, la medición de la altura de un objeto, la creación de gráficos y animaciones en computadora, entre otros.

Ejemplos de problemas resueltos

Hallar la medida de los ángulos de un triángulo rectángulo si se conoce la longitud de sus lados.

Solución:

Supongamos que los lados del triángulo rectángulo son a, b y c, donde c es la hipotenusa y los ángulos opuestos a los lados a, b y c son A, B y C respectivamente. Entonces, por el teorema de Pitágoras, tenemos:

c2 = a2 + b2

Además, sabemos que el ángulo opuesto al lado a es A, el ángulo opuesto al lado b es B y el ángulo opuesto al lado c es C. Por lo tanto, tenemos las siguientes relaciones trigonométricas:

sen A = a/c

cos A = b/c

tan A = a/b

sen B = b/c

cos B = a/c

tan B = b/a

Por lo tanto, podemos hallar los ángulos A y B en función de las longitudes de los lados del triángulo:

sen A = a/c

A = arcsen(a/c)

sen B = b/c

B = arcsen(b/c)

Y, por último, podemos hallar el ángulo C sumando los ángulos A y B y restando el resultado de 180 grados:

C = 180 - A - B

Ejemplo:

Supongamos que tenemos un triángulo rectángulo con lados de longitud a = 3 y b = 4. Queremos hallar la medida de sus ángulos.

Primero, podemos hallar la longitud de la hipotenusa c usando el teorema de Pitágoras:

c2 = a2 + b2 = 32 + 42 = 9 + 16 = 25

c = √ (25) = 5

Luego, podemos hallar los ángulos A y B:

sen A = a/c = 3/5

A = arcsen(3/5) = 36.87 grados

sen B = b/c = 4/5

B = arcsen(4/5) = 53.13 grados

Por último, podemos hallar el ángulo C:

C = 180 - A - B = 180 - 36.87 - 53.13 = 90 grados

Por lo tanto, el triángulo rectángulo tiene ángulos de medida 36.87 grados, 53.13 grados y 90 grados.

¿Por qué aprender acerca de las funciones trigonométricas?

Las funciones trigonométricas son muy importantes en temas técnicos como la ciencia, la ingeniería, la arquitectura, e incluso la medicina. Usted se encontrará con ellos todo el tiempo, así que vale la pena aprenderlas de forma adecuada.

La Topografía es un área de aplicaciones de la trigonometria. Los fabricantes de carreteras, constructores de puentes y aquellos cuyo trabajo consiste en construir aplican de manera profunda ésta área de las matemáticas, la cual usan en su trabajo.




En matemáticas, las funciones trigonométricas (también llamados las funciones circulares) son funciones correspondientes a un ángulo. Ellas se utilizan para relacionar los ángulos de un triángulo y las longitudes de los lados de ese mismo triángulo. Las funciones trigonométricas son importantes en el estudio de los triángulos y los fenómenos que tienen modelos periódicos, entre otras muchas aplicaciones.





Rombo Ejercicios

El Rombo en Matemáticas

En la geometría euclidiana, un rombo (◊),en plural rombos, es un cuadrilátero cuyos cuatro lados tienen la misma longitud. Otro nombre es equilátero cuadrilátero, ya que los medios equiláteros que todos sus lados son iguales. El rombo es a menudo llamado un diamante,

Cada rombo es un paralelogramo, y un rombo con ángulos rectos es un cuadrado. Es decir es en realidad un tipo especial de paralelogramo. Recordemos que en un paralelogramo cada par de lados opuestos tienen igual longitud. En un rombo, los cuatro lados tienen la misma longitud y éste tiene todas las propiedades de un paralelogramo. Ver la definición de un paralelogramo

Es un poco como un cuadrado que puede "inclinarse" y los ángulos interiores no tienen que ser de 90 °. A veces llamado un "diamante" o forma "pastilla".


Introducción al rombo

El rombo es un polígono de cuatro lados, donde los lados opuestos son paralelos y tienen la misma longitud. El rombo tiene cuatro ángulos iguales y diagonales perpendiculares entre sí que se cruzan en su punto medio.

Cálculo del perímetro del rombo

El perímetro de un rombo se calcula sumando las longitudes de sus cuatro lados. Si llamamos a la longitud de cada lado "a", entonces el perímetro será:

Perímetro = 4*a

Cálculo del área del rombo

El área de un rombo se calcula multiplicando la longitud de las diagonales y dividiendo el resultado por 2. Si llamamos a las diagonales "d1" y "d2", entonces el área será:

Área = (d1 * d2) / 2


Ejercicios resueltos

  1. Un rombo tiene un lado de longitud 6 cm y una diagonal de 10 cm. Calcula su perímetro y área.

Para calcular el perímetro, sumamos la longitud de los cuatro lados:

Perímetro = 4 * 6 = 24 cm

Para calcular el área, multiplicamos las dos diagonales y dividimos el resultado por 2:

Área = (6 cm * 10 cm) / 2 = 30 cm2

Por lo tanto, el perímetro del rombo es de 24 cm y su área es de 30 cm^2.

  1. La diagonal de un rombo mide 16 cm y el ángulo que forma con uno de los lados es de 30 grados. Calcula su perímetro y área.

Primero, podemos calcular la longitud de un lado del rombo utilizando trigonometría:

cos(30°) = adyacente / hipotenusa

cos(30°) = a / (16 / 2)

a = (16 / 2) * cos(30°)

a = 6.93 cm (aproximadamente)

Para calcular el perímetro, multiplicamos la longitud de un lado por 4:

Perímetro = 4 * 6.93 cm = 27.72 cm

Para calcular el área, podemos utilizar la fórmula del área en función de las diagonales:

Área = (d1 * d2) / 2

Pero como el rombo es equidiagonal, d1 = d2 = 16 cm. Entonces:

Área = (16 cm * 16 cm) / 2 = 128 cm2

Por lo tanto, el perímetro del rombo es de 27.72 cm y su área es de 128 cm2


Variables Separables Ejercicios Resueltos

Variables Separables

Variables separables en ecuaciones diferenciales

Las ecuaciones diferenciales son una parte fundamental de las matemáticas y se utilizan para modelar una amplia variedad de fenómenos en la física, la ingeniería, la economía y otras áreas. Una de las formas más comunes de ecuación diferencial es la ecuación diferencial ordinaria (EDO), que se utiliza para modelar la relación entre una función y su derivada. 

Una forma especial de EDO es la ecuación diferencial separable, que se puede resolver utilizando la técnica de variables separables.

¿Qué son las ecuaciones diferenciales separables?

Una EDO separable es una ecuación que se puede escribir en la forma:

dy/dx = f(x)g(y)

Donde f(x) y g(y) son funciones de x e y, respectivamente. La clave para resolver una EDO separable es separar las variables x e y, de modo que todas las x estén en un lado de la ecuación y todas las y estén en el otro lado. Esto se puede hacer mediante la técnica de la multiplicación cruzada, que implica la multiplicación de ambos lados de la ecuación por el denominador de una de las funciones. Luego, se integra cada lado por separado para obtener la solución.

Pasos para resolver una ecuación diferencial separable

Los pasos generales para resolver una ecuación diferencial separable son los siguientes:

  1. Escribir la ecuación en la forma dy/dx = f(x)g(y).
  2. Separar las variables x e y.
  3. Integrar ambos lados de la ecuación por separado.
  4. Añadir la constante de integración C.
  5. Si es necesario, despejar y para obtener la solución explícita.

Ejemplos resueltos de ecuaciones diferenciales separables

  1. Resolver la ecuación diferencial separable dy/dx = x2 y.

Solución:

dy/y = x2 dx Integrando ambos lados obtenemos: ln|y| = x3/3 + C Despejando y:

y = e^(x3/3+C) = Ke^(x3/3), donde K = +/-ec es la constante de integración.

  1. Resolver la ecuación diferencial separable dy/dx = y2/x.

Solución:

dy/y2 = dx/x Integrando ambos lados obtenemos: -1/y = ln|x| + C Despejando y: y = -1/(ln|x| + C), donde C es la constante de integración.

  1. Resolver la ecuación diferencial separable dy/dx = xcos(y).

Solución:

dy/cos(y) = x dx Integrando ambos lados obtenemos: sen(y) = x2/2 + C Despejando y: y = arcsen(x2/2 + C), donde C es la constante de integración.

 

Ejercicios resueltos

  1. Resolver la ecuación diferencial dy/dx = 2xy, con y(0) = 1.

Solución:

Primero, separamos las variables en la ecuación:

dy/y = 2x dx

Integramos ambos lados:

∫(dy/y) = ∫(2x dx)

ln|y| = x2 + C

donde C es una constante de integración.

Despejando y:

|y| = e^(x2 + C) = eC * e^(x2)

y = ± eC * e^(x2)

Usando la condición inicial y(0) = 1, tenemos:

1 = ± eC * e0

1 = ± eC

Por lo tanto, C = 0 y la solución a la ecuación diferencial es:

y = e^(x2)

  1. Resolver la ecuación diferencial dy/dx = 3x2 y2, con y(1) = -1.

Solución:

Nuevamente, separamos las variables:

dy/y2 = 3x2 dx

Integramos ambos lados:

∫(dy/y2) = ∫(3x2 dx)

-1/y = x3 + C

Despejando y:

y = -1 / (x3 + C)

Usando la condición inicial y(1) = -1, tenemos:

-1 = -1 / (13 + C)

C = 0

Por lo tanto, la solución a la ecuación diferencial es:

y = -1 / x3

  1. Resolver la ecuación diferencial dy/dx = (2x + 1) / y, con y(0) = 1.

Solución:

Separamos las variables:

y dy = (2x + 1) dx

Integramos ambos lados:

∫(y dy) = ∫((2x + 1) dx)

Y2 / 2 = x2 + x + C

Despejando y:

y = ± Raíz cuadrada (2x^2 + 2x + 2C)

Usando la condición inicial y(0) = 1, tenemos:

1 = ± Raíz cuadrada (2(0)2 + 2(0) + 2C)

1 = ± Raíz cuadrada (2C)

C = 1/2

Por lo tanto, la solución a la ecuación diferencial es:

y = Raíz cuadrada (2x^2 + 2x + 1)


Aplicaciones de la primera y segunda derivada en ecuaciones diferenciales

La primera y segunda derivada de una función tienen importantes aplicaciones en ecuaciones diferenciales y en problemas de optimización. A continuación, se presentan algunos ejemplos de cómo se pueden aplicar las derivadas en ecuaciones diferenciales.

Problema de la ley de enfriamiento de Newton

La ley de enfriamiento de Newton se utiliza para modelar el proceso de enfriamiento de un objeto a temperatura ambiente. La ecuación diferencial para la temperatura de un objeto que se enfría en un ambiente a temperatura constante se puede escribir como:

dT/dt = -k(T - Ta)

donde T es la temperatura del objeto, Ta es la temperatura ambiente y k es una constante de proporcionalidad. La solución a esta ecuación diferencial es:

T(t) = Ta + (T0 - Ta) e-kt

donde T0 es la temperatura inicial del objeto en el tiempo t=0.

Para maximizar la tasa de enfriamiento del objeto, debemos encontrar el valor de t para el cual la tasa de cambio de la temperatura es máxima. Para ello, podemos utilizar la primera y segunda derivada de la función T(t). La primera derivada es:

dT/dt = -k(T0 - Ta) e-kt

La segunda derivada es:

d2 /dt2 = k2(T0 - Ta) e-kt

Para maximizar la tasa de enfriamiento, debemos encontrar el valor de t para el cual la segunda derivada es igual a cero. Resolviendo la ecuación d^2T/dt^2 = 0, obtenemos:

t = ln(2)/k

Por lo tanto, el tiempo necesario para maximizar la tasa de enfriamiento es ln(2)/k.