Menú

▼

PÁGINAS

▼

7.4.23

EJERCICIOS RESUELTOS DE PROGRESION GEOMETRICA

EJERCICIOS DE PROGRESIÓN GEOMÉTRICA

Una progresión geométrica que es también conocida como una secuencia geométrica, es sencillamente una secuencia de números, donde cada término después del primero se encuentra multiplicando el anterior por un número fijo distinto de cero llamado la razón común. 

Ejemplo, la secuencia de 2, 8, 32, 128, ... es una progresión geométrica con razón común de 4. Del mismo modo 10, 5, 2.5, 1.25, ... es una secuencia geométrica con razón común 1/2.

Ejemplos de una secuencia geométrica se pueden establecer con una potencia:  rk de un número r fijo, como  2k y 5k

Forma general de una progresión geométrica

a,\ ar,\ ar^2,\ ar^3,\ ar^4,\ \ldots

donde r ≠ 0 es la razón común y a es un factor de escala, igual a valor de inicio de la secuencia.

El término enésimo de una progresión geométrica con un valor inicial y razón común r está dada por

a_n = a\,r^{n-1}.

 Tal secuencia geométrica también sigue la relación establecida como:

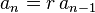 a_n = r\,a_{n-1}  donde n es un entero y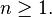  n\geq 1.

Generalmente, para comprobar si una secuencia dada es geométrico, uno simplemente comprueba si las entradas sucesivas en la secuencia de todas tienen la misma relación.

La razón común de una serie geométrica puede ser negativa, lo que resulta en una secuencia alterna, con los números de conmutación de positivo a negativo y viceversa. Por ejemplo:

1, -3, 9, -27, 81, -243, ...
es una secuencia geométrica con relación común de -3.

EJERCICIOS RESUELTOS DE PROGRESIÓN GEOMÉTRICA

Presentamos algunos problemas resueltos paso a paso para reforzar y afianzar los procedimientos. El vídeo muestra varios aspectos importantes.

El comportamiento de una secuencia geométrica depende del valor de la razón común.Si la relación común es:


  • Positiva, los términos serán todos del mismo signo que el término inicial.
  • Negativa, los términos se alternarán entre positivo y negativo.
  • Mayor que 1, habrá un crecimiento exponencial hacia el infinito positivo o negativo (según el signo del término inicial).
  • 1, la progresión es una secuencia constante.
  • Entre -1 y 1, pero no cero, habrá decaimiento exponencial a cero.
  • -1, La progresión es una secuencia alterna
  • Menos de -1, para los valores absolutos hay un crecimiento exponencial hacia (sin signo) el infinito, debido a la señal alterna.

PROBLEMAS RESUELTOS DE PROGRESIONES GEOMÉTRICAS

Un resultado interesante de la definición de una progresión geométrica es que para cualquier valor de la razón común, cualquiera de los tres aspectos consecutivos a, b y c tendrán que satisfacer la siguiente ecuación:


 b^2=ac

donde b se considera que es la media geométrica entre a y c.

EJERCICIOS RESUELTOS DE PROGRESIÓN ARITMÉTICA Y PROGRESIÓN GEOMÉTICA

Veamos en un mismo vídeo tanto la progresión aritmética como la progresión geométrica y encontrar las semejanzas y las diferencias entre éstas dos secuencias.



Serie geométrica

Una serie geométrica es la suma de los números en una progresión geométrica. Por ejemplo:


 2 + 10 + 50 + 250 = 2 + 2 \times 5 + 2 \times 5^2 + 2 \times 5^3. \,

Si tenemos que el primer término (en este caso 2), m el número de términos (en este caso 4), y r sea la constante de que cada término se multiplica por conseguir la próxima cantidad (en este caso 5), la suma está dada por:


 \frac{a(1-r^m)}{1-r}

En el ejemplo anterior, si resolvemos con la fórmula planteada, tenemos que:


 2 + 10 + 50 + 250 = \frac{2(1-5^4)}{1-5} = \frac{-1248}{-4} = 312.