Menú

▼

PÁGINAS

▼

3.6.14

EJERCICIOS DE SUMA Y RESTA DE MATRICES

EJERCICIOS RESUELTOS DE SUMA Y RESTA DE MATRICES

Ejemplo: una matriz con 3 filas y 5 columnas se puede añadir a otra matriz de 3 filas y 5 columnas.
Pero no se podría agregar a una matriz con 3 filas y 4 columnas (puesto que las columnas no coinciden en tamaño)

 La suma de matrices es la operación de sumar dos matrices mediante la adición de las entradas correspondientes juntas.

 EJERCICIOS RESUELTOS

\begin{bmatrix} 1 & 3 \\ 1 & 0 \\ 1 & 2 \end{bmatrix} + \begin{bmatrix} 0 & 0 \\ 7 & 5 \\ 2 & 1 \end{bmatrix} = \begin{bmatrix} 1+0 & 3+0 \\ 1+7 & 0+5 \\ 1+2 & 2+1 \end{bmatrix} = \begin{bmatrix} 1 & 3 \\ 8 & 5 \\ 3 & 3 \end{bmatrix}

También podemos restar una matriz de otra, siempre que tengan las mismas dimensiones.

 A - B se calcula restando elementos correspondientes de A y B, y tiene las mismas dimensiones que A y B. Por ejemplo:

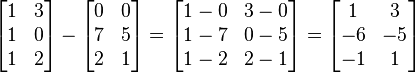
\begin{bmatrix} 1 & 3 \\ 1 & 0 \\ 1 & 2 \end{bmatrix} - \begin{bmatrix} 0 & 0 \\ 7 & 5 \\ 2 & 1 \end{bmatrix} = \begin{bmatrix} 1-0 & 3-0 \\ 1-7 & 0-5 \\ 1-2 & 2-1 \end{bmatrix} = \begin{bmatrix} 1 & 3 \\ -6 & -5 \\ -1 & 1 \end{bmatrix}

SUMA Y RESTA DE MATRICES

En el siguiente vídeo se consignan más ejemplos de suma y resta con matrices de mayor tamaño ( matrices 3x3)


Matriz: Suma y Resta

Las matrices se pueden sumar o restar la una de la otra solamente si tienen el mismo tamaño, lo que significa que tienen que tener el mismo número de filas y columnas. Esto se debe a que al añadir o restar matrices, los operadores trabajan en las entradas correspondientes de las matrices, de ahí la necesidad del mismo tamaño.

 Veamos la forma de la Matrix, como se muestra en estas dos matrices A y B de tamaño 2 x 2









EJERCICIO RESUELTO