Los Números Enteros | Ejercicios Resueltos
Enteros Positivos y Enteros Negativos
Los números enteros son aquellos números que no tienen decimales ni fracciones, es decir, son números completos que se utilizan para contar objetos o representar magnitudes enteras. Los números enteros pueden ser positivos, negativos o cero, y se representan en la recta numérica como puntos separados por una unidad.
Los números enteros se representan por la letra "Z" en matemáticas y abarcan desde el cero hacia la derecha (números positivos) y hacia la izquierda (números negativos). Por ejemplo, los primeros números enteros positivos son: 1, 2, 3, 4, 5, etc. Los primeros números enteros negativos son: -1, -2, -3, -4, -5, etc. El número cero, que no es positivo ni negativo, también se considera un número entero.
Para indicar si un objeto se encuentra a la derecha o a la izquierda de un punto de referencia, podemos indicar con un signo (+) si está hacia la derecha y con un signo (-) si se ubica hacia la izquierda. De esta forma obtenemos dos conjuntos:
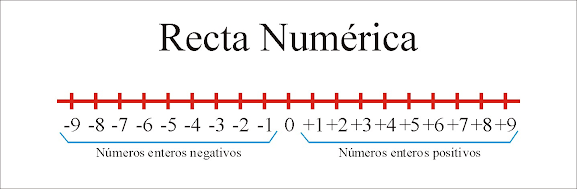
Recta Numérica
La recta numérica de números enteros es una herramienta fundamental en matemáticas para representar y comprender los números enteros en una línea recta. Es una línea que se extiende en ambas direcciones infinitamente y que se divide en pequeñas unidades de medida iguales, cada una representando un número entero.
En la recta numérica de números enteros, el número cero se encuentra en el centro de la línea, y los números positivos se ubican hacia la derecha del cero, mientras que los números negativos se ubican hacia la izquierda del cero. Cada número entero se representa como un punto en la línea, separado por una unidad de distancia de los demás puntos.
Esta herramienta es muy útil para la comparación de números enteros y para representar operaciones matemáticas como la suma y la resta. Por ejemplo, si se desea sumar dos números enteros, se ubica el primer número en la recta numérica y se cuenta hacia la derecha la cantidad de unidades que representa el segundo número, lo que dará como resultado la ubicación del resultado de la suma.
La recta numérica de números enteros también permite visualizar las propiedades de los números enteros, como la propiedad conmutativa de la suma y la resta, y la propiedad distributiva de la multiplicación sobre la suma. Además, es una herramienta útil para la resolución de problemas matemáticos y la comprensión de conceptos matemáticos como la comparación de números enteros, la identificación de patrones y la representación de situaciones reales.
Los números enteros son fundamentales en las matemáticas, ya que se utilizan en diversas ramas como la aritmética, el álgebra y la geometría. Además, son útiles para representar situaciones en el mundo real, como el número de personas en una habitación o la temperatura en un determinado lugar.
VALOR ABSOLUTO
El valor absoluto de una cantidad a, se denota por la expresión: |a|.
Este valor puede considerarse como la distancia que hay desde el número en
cuestión hasta el cero. Observe en la recta que la distancia que hay desde el -3 hasta el 0 es 3 unidades, por esto el valor absoluto de -3 es 3 y de manera similar la distancia que existe entre el 4 y el 0 es 4, lo anterior se puede escribir como:
Esto
es, el valor absoluto de:
a)
un número entero positivo es el mismo entero
positivo.
b)
un número entero negativo es su simétrico.
c)
el cero es el mismo cero
A diferencia de los naturales, para efectuar la adición y
sustracción con ellos,se
emplea el valor absoluto y el simétrico de un
número.
Ejemplos:
a) | 200 | esto se le "valor absoluto de 200 y el resultado es 200".b) | -756 | esto se lee "valor absoluto de -756 y el resultado es 756".
En conclusión:
Valor absoluto de un número entero
El valor absoluto de un número entero es el
número natural
que resulta al suprimir su signo.
El valor absoluto lo escribiremos entre barras
verticales.
Ejemplo:
|−5| = 5
|5| = 5
|
Opuesto de un número:
Es el número que sumado a otro da como resultado cero.
Ejemplos:
96, su opuesto es -96; si se suman 96 + (-96) = 0
-353, su opuesto es 353; si se suman -353 + 353 = 0
Ya que se tiene presente cómo determinar el valor absoluto y opuesto de un
número, se pueden realizar las adiciones y sustracciones con números enteros.
Pero antes hablaremos de su representación y el orden.
Representación de los números enteros
1. En una recta horizontal, se toma un punto cualquiera que se señala como cero.
2. A su derecha y a distancias iguales se van señalando los números positivos: 1, 2,
3. A la izquierda del cero y a distancias iguales que las anteriores, se van
señalando los números negativos: −1, −2, −3, ...
Orden en los números enteros
Los números enteros están ordenados. De dos números representados gráficamente, es mayor el que está situado más a la derecha, y menor el situado más a la izquierda.
1. Todo número negativo es menor que cero.
−7 < 0
2. Todo número positivo es mayor que cero.
7 > 0
3. De dos enteros negativos es mayor el que tiene menor valor absoluto.
−7 > −10
|−7| < |−10|
4. De los enteros positivos, es mayor el que tiene mayor valor absoluto.
10 > 7
|10| > |7|
El conjunto formado por los números positivos, los números negativos y el cerose llama conjunto de números enteros.
En resumen, los números enteros son aquellos números que no tienen decimales ni fracciones y se utilizan para contar objetos o representar magnitudes enteras. Estos números pueden ser positivos, negativos o cero y son fundamentales en las matemáticas y la representación de situaciones en el mundo real.