7.4.23

Home » , , » EJERCICIOS DE MULTIPLICACIÓN DE MATRICES

EJERCICIOS DE MULTIPLICACIÓN DE MATRICES

By  Didacticol   7:57  

EJERCICIOS DE MULTIPLICACIÓN DE MATRICES

Como multiplicar dos matrices

La multiplicación de matrices se divide en dos categorías generales:

Por un escalar en los que un número se multiplica con cada entrada de una matriz.

Multiplicación de toda una matriz por otra matriz entera, la multiplicación de matrices en ésta entrada se referirá a esta segunda categoría.

¿Qué es la multiplicación de la matriz?

Usted puede multiplicar dos matrices si, y sólo si, el número de columnas de la primera matriz es igual al número de filas de la segunda matriz.

De lo contrario, el producto de dos matrices no está definido.
Las dimensiones de la matriz producto son:

 (filas de la primera matriz) × (columnas de la segunda matriz)

EJERCICIO RESUELTO


\begin{pmatrix} 2 &0 \\ 4 &6 \\ 8 &2 \end{pmatrix} \begin{pmatrix} 1 &3 \\ 5 &7 \end{pmatrix} = \begin{pmatrix} 2\cdot 1+0\cdot 5 &2\cdot 3+0\cdot 7 \\ 4\cdot 1+6\cdot 5 &4\cdot 3+6\cdot 7 \\ 8\cdot 1+2\cdot 5 &8\cdot 3+2\cdot 7 \end{pmatrix} = \begin{pmatrix} 2 &6 \\ 34 &54 \\ 18 &38 \end{pmatrix}

La multiplicación de matrices casi nunca es conmutativa. Veamos que pasa al multiplicar matrices en ambos sentidos.


\begin{pmatrix} 1 &2 \\ 3 &4 \end{pmatrix} \begin{pmatrix} 5 &6 \\ 7 &8 \end{pmatrix} = \begin{pmatrix} 19 &22 \\ 43 &50 \end{pmatrix} \qquad \begin{pmatrix} 5 &6 \\ 7 &8 \end{pmatrix} \begin{pmatrix} 1 &2 \\ 3 &4 \end{pmatrix} = \begin{pmatrix} 23 &34 \\ 31 &46 \end{pmatrix}

EJERCICIOS RESUELTOS EN VÍDEO

Introducción: podemos estudiar los conceptos preliminares sobre las matrices y su orden; esto nos permitirá manejar de forma adecuada los conceptos básicos.

Cómo multiplicar matrices

Una matriz es un arreglo rectangular de números, símbolos o expresiones en filas y columnas. Para multiplicar matrices, tendrá que multiplicar los elementos (o números) de la fila de la primera matriz por los elementos de las filas de la segunda matriz. Puede multiplicar matrices en tan sólo unos sencillos pasos que veremos a continuación en el siguiente vídeo.

En términos generales tenemos que la multiplicación de dos matrices no es conmutativa, esto es:

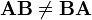
\mathbf{A}\mathbf{B} \neq \mathbf{B}\mathbf{A}

EJERCICIO DE MULTIPLICACIÓN DE MATRICES


\begin{align} \begin{pmatrix} {\color{Brown}1} & {\color{Orange}2} & {\color{Violet}3} \\ {\color{Brown}4} & {\color{Orange}5} & {\color{Violet}6} \\ {\color{Brown}7} & {\color{Orange}8} & {\color{Violet}9} \\ \end{pmatrix} \begin{pmatrix} {\color{Brown}a} & {\color{Brown}d} \\ {\color{Orange}b} & {\color{Orange}e} \\ {\color{Violet}c} & {\color{Violet}f} \\ \end{pmatrix} &= \begin{pmatrix} {\color{Brown}1} \\ {\color{Brown}4} \\ {\color{Brown}7} \\ \end{pmatrix} \begin{pmatrix} {\color{Brown}{a}} & {\color{Brown}{d}} \\ \end{pmatrix} + \begin{pmatrix} {\color{Orange}2} \\ {\color{Orange}5} \\ {\color{Orange}8}\\ \end{pmatrix} \begin{pmatrix} {\color{Orange}{b}} & {\color{Orange}{e}} \\ \end{pmatrix}+ \begin{pmatrix} {\color{Violet}3} \\ {\color{Violet}6} \\ {\color{Violet}9} \\ \end{pmatrix} \begin{pmatrix} {\color{Violet}c} & {\color{Violet}f} \\ \end{pmatrix} \\&= \begin{pmatrix} {\color{Brown}{1a}} & {\color{Brown}{1d}} \\ {\color{Brown}{4a}} & {\color{Brown}{4d}} \\ {\color{Brown}{7a}} & {\color{Brown}{7d}} \\ \end{pmatrix}+ \begin{pmatrix} {\color{Orange}{2b}} & {\color{Orange}{2e}} \\ {\color{Orange}{5b}} & {\color{Orange}{5e}} \\ {\color{Orange}{8b}} & {\color{Orange}{8e}} \\ \end{pmatrix}+ \begin{pmatrix} {\color{Violet}{3c}} & {\color{Violet}{3f}} \\ {\color{Violet}{6c}} & {\color{Violet}{6f}} \\ {\color{Violet}{9c}} & {\color{Violet}{9f}} \\ \end{pmatrix} \\&= \begin{pmatrix} {\color{Brown}{1a}} + {\color{Orange}{2b}} + {\color{Violet}{3c}} & {\color{Brown}{1d}} + {\color{Orange}{2e}} + {\color{Violet}{3f}} \\ {\color{Brown}{4a}} + {\color{Orange}{5b}} + {\color{Violet}{6c}} & {\color{Brown}{4d}} + {\color{Orange}{5e}} + {\color{Violet}{6f}} \\ {\color{Brown}{7a}} + {\color{Orange}{8b}} + {\color{Violet}{9c}} & {\color{Brown}{7d}} + {\color{Orange}{8e}} + {\color{Violet}{9f}} \\ \end{pmatrix}. \end{align}

¿Qué es Matrix?

La multiplicación de matrices no cumple con la propiedad conmutativa. Al Multiplicar A x B y B x A,  se presentan resultados diferentes. La multiplicación de matrices es la operación más útil y más común que se encuentra en las aplicaciones de algunos campos profesionales como la química.

Una matriz es un arreglo de números en filas y columnas que puede ser cuadrada, a menudo rectangular. 

Se puede establecer las dimensiones como m x n, donde (m) se refieren al número de filas y (n) al número de columnas. Los valores individuales que constituyen una matriz son conocidos como sus elementos, generalmente contemplados en filas y columnas. 

Como hemos expresado, las matrices tienen una variedad de aplicaciones; por ejemplo en química, también en el ajuste de curvas y en la mecánica cuántica o la teoría de grupos y gráficos moleculares. 

En la multiplicación de la matriz AxB, el número de columnas de la matriz A debe ser igual al número de filas de la matriz B. La matriz producto resultante tendrá el mismo número de filas que la matriz A y el mismo número de columnas que B.

Matriz identidad multiplicativa

La matriz identidad multiplicativa es una matriz que podemos multiplicar por otra matriz y la matriz resultante será igual a la matriz original.

Propiedades de la multiplicación

1. Cuando trabajamos con matrices, la multiplicación no es conmutativa.

AB ≠ BA

2. la multiplicación de matrices es asociativa. No importa cómo se agrupen tres o más matrices, cuando estas se multiplican, el resultado no cambia.

A(BC) = (AB) C

3. La multiplicación de matrices es asociativa, esto es análogo a la multiplicación algebraica simple. La única diferencia es que se mantenga el orden de la multiplicación.

A(B+C) = AB + AC ≠ (B + C) A = BA + CA

4. Si es una matriz cuadrada, existe un elemento de identidad para la multiplicación de la matriz. Se llama I

IA = IA = A


Las Matrices son ampliamente utilizadas en aplicaciones de gráficos de geometría, física e informática. En muchas aplicaciones es necesario calcular la multiplicación de la matriz 3 x 3.

Características de las Matrices

  • Las matrices son un arreglo rectangular de elementos, dispuestos en filas y columnas.
  • Las matrices pueden ser de distintas dimensiones, es decir, pueden tener diferentes números de filas y columnas.
  • Las matrices pueden ser clasificadas según su forma. Una matriz es cuadrada si tiene el mismo número de filas y columnas, y es rectangular en caso contrario.
  • Las matrices pueden ser clasificadas según sus elementos. Una matriz es nula si todos sus elementos son cero, y es identidad si tiene unos en su diagonal principal y ceros en el resto de sus elementos.
  • Las operaciones básicas que se pueden realizar con matrices incluyen la suma y la multiplicación.
  • La suma de dos matrices se realiza sumando elemento por elemento.
  • La multiplicación de dos matrices se realiza multiplicando filas por columnas y sumando los productos resultantes.
  • Las matrices también se pueden multiplicar por un escalar, es decir, por un número.
  • Las matrices pueden ser transpuestas, es decir, cambiando filas por columnas y viceversa.
  • Las matrices pueden ser invertibles o no invertibles, según si existe o no una matriz inversa que al multiplicarse por la matriz original de como resultado la matriz identidad.
  • Las matrices tienen aplicaciones en distintas ramas de las matemáticas y en otros campos como la física, la informática y la economía.